Вучэбны дапаможнік для студэнтаў фізічнага і радыёфізічнага факультэтаў у пяці частках, страница 7

1.78.  Прылада складаецца з пяці элементаў, з якіх два сапсаваныя. Пры ўключэнні прылады выпадкова ўключаюцца два элементы. Знайдзіце імавернасць таго, што ўключанымі будуць несапсаваныя элементы.

1.79.  У групе 12 студэнтаў, сярод якіх 4 выдатнікі. Знайдзіце імавернасць таго, што сярод 9 выпадкова адабраных студэнтаў трое выдатнікаў.

1.80.  У гульні “Спортлато” 6 нумароў з 49 ёсць “шчаслівыя”. Удзельнік гульні адзначае 6 нумароў з 49. Якая імавернасць адгадаць: 1) усе 6 “шчаслівых” нумароў; 2) тры ”шчаслівыя” нумары?

1.81.  Запішыце расклад паводле формулы бінома Ньютана: 1)(1 + x)⁷;   2)(x+ y)⁵;   3)(x– y)⁵;   4)(2 – a)⁷;   5)(2x+ 3y)⁷;   6).

1.82.  Дакажыце, што  пры  i  пры .

1.83.  Вызначце n так, каб каэфіцыенты пры x⁵ і x¹² з раскладу бінома  былі роўнымі.

1.84.  Знайдзіце каэфіцыент раскладу бінома: 1) 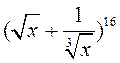    пры x³; 2) пры x²; 3)   пры x⁴.

1.85.  Знайдзіце вольны складнік раскладу бінома: 1) ;     2) ;    3) .

1.86.  Дакажыце, што сума каэфіцыентаў раскладу бінома  пры кожным натуральным n роўная адзінцы.

1.87.  Сума каэфіцыентаў раскладу бінома 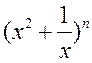 роўная 1024. Знайдзіце каэфіцыент раскладу бінома пры х¹¹.

1.88.  Знайдзіце каэфіцыент мнагаскладу: 1) (1 + x + x²)³ пры x³; 2) (1 + 2x– 3x²)⁴ пры x³; 3) (1 + x² – x³)⁹ пры x⁸; 4) (1 + x² + x³)⁷ пры x¹¹.

1.89.  Знайдзіце складнікі раскладу бінома, якія з’яўляюцца цэлымі лікамі:  1) ;     2) ;      3) .

1.90.  Колькі рацыянальных складнікаў змяшчаецца ў раскладзе бінома ?

1.91.  У раскладзе бінома 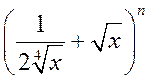 першыя тры каэфіцыенты ўтва-раюць арыфметычную прагрэсію. Знайдзіце ўсе рацыянальныя складнікі бінома.

1.92.  Дакажыце, што для ўсіх натуральных n: 1) n³ – n  дзеліцца на 3; 2) n⁵ – n дзеліцца на 5; 3) n⁷ – n дзеліцца на 7; 4) n¹¹ – n дзеліцца на 11.

1.93.  Дакажыце тэарэму Фэрма: калі p ёсць просты лік, то розніца n^p – n дзеліцца на p, для кожнага натуральнага n.

1.4. МНАГАСКЛАДЫ

1º. Мнагаскладам або паліномам n-й ступені называюць выраз

, дзе каэфіцыенты  ёсць камплексныя лікі і зменная z набывае значэнні з мноства  камплексных лікаў. У прыватнасці, як , так і zмогуць быць рэчаіснымі. Два мнагасклады тоесна роўныя адзін аднаму, калі і толькі калі роўныя іх ступені і каэфіцыенты пры аднолькавых ступенях z.

Для кожных двух мнагаскладаў  і , існуюць мнага-склады  і , такія, што =. Мнагасклад  называюць дзеллю, а мнагасклад  – астачай ад дзялення мнагаскладу  на мнагасклад . Калі мнагасклад , то кажуць, што  дзеліцца на , пры гэтым мнагасклад  называюць дзельнікам мнагаскладу .

Лік а называюць коранем мнагаскладу , калі .

Тэарэма Бэзу. Лік а ёсць корань мнагаскладу , калі і толькі калі гэты мнагасклад дзеліцца на , г. зн. .

Калі існуюць лік  і мнагасклад  такія, што для ўсіх  выконваецца роўнасць , то лік а называецца коранем мнагаскладу  кратнасці k .

Тэарэма Гаўса. Усякі мнагасклад n-й ступені на мностве камплексных лікаў мае n каранёў, калі кожны k–кратны корань лічыцца k разоў.

З тэарэмы Гаўса вынікае, што кожны мнагасклад  можна падаць у выглядзе

,                    (1.11)

дзе  – розныя карані мнагаскладу, а .

Калі камплексны лік  ёсць корань кратнасці  мнагаскладу  з рэчаіснымі каэфіцыентамі, то спалучаны лік  таксама ёсць корань кратнасці  мнагаскладу . Калі ў (1.11) перамножыць множнікі, якія адпавядаюць спалучаным караням, то роўнасць (1.11) набывае выгляд

,  (1.12)

дзе  

Прыклад 1. Развязаць раўнанне .

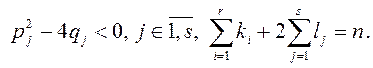
►Карыстаючыся формулай вылічэння каранёў квадратовага раўнання, знаходзім . ◄

Прыклад 2. Развязаць раўнанне .

►Паводле формулы вылічэння каранёў квадратовага раўнання маем  . На падставе прыкладу 5 §1.2 атрымаем .◄

Прыклад 3. Запісаць мнагасклад  у выглядзе здабытку двух мнагаскладаў другой ступені з рэчаіснымі каэфіцыентамі.

►Спосаб першы. Паводле формулы (1.9) вылічым : . У такім разе мнагасклад  можна падаць у  выглядзе . Перамнажаючы папарна лі-нейныя множнікі, што адпавядаюць камплексна спалучаным караням, атрымаем .