1.14. Вылічыце: 1) 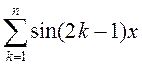 ; 2)
; 2) 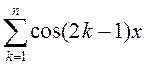 ; 3)
; 3) 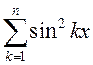 ;
4)
;
4) 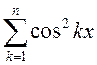 ; 5)
; 5) 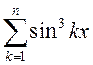 ; 6)
; 6) 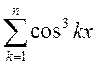 .
.
1.15.
Дакажыце, што роўнасць праўдзіцца пры ўсякім n, ![]() :
1)
:
1) 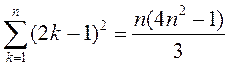 ; 5)
; 5) 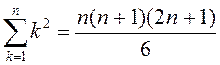 ;
2)
;
2) 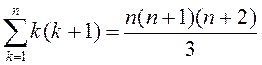 ; 6)
; 6)  ;
3)
;
3) 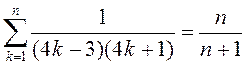 ; 7)
; 7) 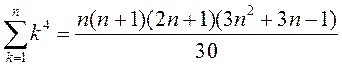 ;
4)
;
4) 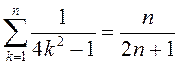 ; 8)
; 8) 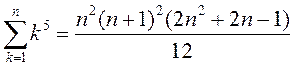 .
.
1.16.
Дакажыце, што для n – га элемента арыфметычнай прагрэсіі ![]() з
розніцай
з
розніцай ![]() і сумы яе
і сумы яе ![]() элементаў
элементаў ![]() праўдзяцца формулы:
праўдзяцца формулы: ![]()
![]() .
.
1.17.
Дакажыце, што для n – га элемента геаметрычнай прагрэсіі ![]() з
назоўнікам q і сумы яе
з
назоўнікам q і сумы яе ![]() элементаў
элементаў ![]() праўдзяцца формулы:
праўдзяцца формулы: ![]()
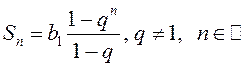 .
.
1.18.
Дакажыце, што для ўсякіх рэчаісных лікаў ![]() , мае месца няроўнасць
, мае месца няроўнасць ![]() .
.
1.19.
Дакажыце, што пры кожным ![]() праўдзяцца няроўнасці:
1)
праўдзяцца няроўнасці:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
1.20.
Высветліце, пры якіх натуральных n справядлівыя
няроўнасці:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() ;
6)
;
6) ![]() .
.
1.21.
Дакажыце няроўнась Бэрнулі ![]() .
.
1.22.
Дакажыце, што пры кожным натуральным n лік ![]() кратны
ліку b:
1)
кратны
ліку b:
1) ![]() , b = 7; 2)
, b = 7; 2) ![]() , b = 6;
3)
, b = 6;
3) ![]() , b = 3;
4)
, b = 3;
4) ![]() , b =5; 5)
, b =5; 5) ![]() , b =9; 6)
, b =9; 6) ![]() ,
, ![]() .
.
1.23.
Дакажыце, што пры кожным натуральным n лік 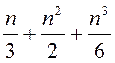 ёсць цэлы.
ёсць цэлы.
1.24.
Дакажыце, што пры кожным натуральным n лік 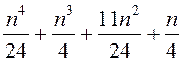 з’яўляецца
натуральным.
з’яўляецца
натуральным.
1º. Бясконцы
дзесятковы дроб называецца рэчаісным лікам. Мноства рэчаісных
лікаў абазначаецца ![]() .
.
Лікі ![]() ,
дзе
,
дзе ![]() ,
, ![]() называюцца
рацыянальнымі, а сам выраз
называюцца
рацыянальнымі, а сам выраз ![]() – рацыянальным дробам.
Мноства ўсіх рацыянальных лікаў
абазначаецца
– рацыянальным дробам.
Мноства ўсіх рацыянальных лікаў
абазначаецца ![]() . Кожны рацыянальны лік можна
запісаць як дзесятковы дроб. Бясконцыя дзесятковыя перыядычныя дробы і толькі
яны ёсць рацыянальныя лікі. Рэчаісны лік, які не ёсць рацыянальны, называецца ірацыянальным.
. Кожны рацыянальны лік можна
запісаць як дзесятковы дроб. Бясконцыя дзесятковыя перыядычныя дробы і толькі
яны ёсць рацыянальныя лікі. Рэчаісны лік, які не ёсць рацыянальны, называецца ірацыянальным.
2º. Няхай X ёсць падмноства мноства рэчаісных лікаў, ![]() . Мноства X называецца абмежаваным зверху (знізу),
калі існуе такі рэчаісны лік
. Мноства X называецца абмежаваным зверху (знізу),
калі існуе такі рэчаісны лік ![]() , што для
ўсіх
, што для
ўсіх ![]() праўдзіцца няроўнасць
праўдзіцца няроўнасць ![]()
![]() ;
лік A (a) называецца верхняй мяжой
(ніжняй мяжой) мноства Х. Мноства, абмежаванае зверху і
знізу, называецца абмежаваным. Найменшая (найбольшая) з усіх
канечных або бясконцых верхніх (ніжніх) межаў мноства
;
лік A (a) называецца верхняй мяжой
(ніжняй мяжой) мноства Х. Мноства, абмежаванае зверху і
знізу, называецца абмежаваным. Найменшая (найбольшая) з усіх
канечных або бясконцых верхніх (ніжніх) межаў мноства ![]() называецца дакладнай
верхняй (ніжняй) мяжой мноства X і абазначаецца
называецца дакладнай
верхняй (ніжняй) мяжой мноства X і абазначаецца ![]() (
(![]() ).
).
Калі M = ![]() (m =
(m = ![]() ),
то:
),
то:
1) ![]() выконваецца
няроўнасць
выконваецца
няроўнасць ![]() ;
;
2) ![]() такі, што
такі, што ![]() .
.
Калі m і M ёсць канечныя лікі, то ўмова 2) раўназначная таму, што
![]() такі, што
такі, што ![]() (
(![]() ).
).
Тэарэма пра межы. Кожнае абмежаванае зверху (знізу) непустое мноства рэчаісных лікаў мае канечную дакладную верхнюю (ніжнюю) мяжу.
3º. Алгебраічнай формай камплекснага ліку z называецца выраз ![]() , дзе x, y – рэчаісныя лікі, i –
уяўнаяадзінка. Рэчаісныя лікі x і y называ-юцца адпаведна рэчаіснай і ўяўнай
часткамі ліку z і абазначаюцца x= Re z, y= Im z.
Два камплексныя лікі
, дзе x, y – рэчаісныя лікі, i –
уяўнаяадзінка. Рэчаісныя лікі x і y называ-юцца адпаведна рэчаіснай і ўяўнай
часткамі ліку z і абазначаюцца x= Re z, y= Im z.
Два камплексныя лікі ![]() і
і ![]() называюцца роўнымі,
калі і толькі калі
называюцца роўнымі,
калі і толькі калі ![]() . Камплексны лік x–
iy называецца спалучаным
камплекснаму ліку x+ iу і
абазначаецца
. Камплексны лік x–
iy называецца спалучаным
камплекснаму ліку x+ iу і
абазначаецца ![]() .
.
Арыфметычныя дзеянні з камплекснымі лікамі ![]() i
i ![]() выконваюцца паводле правілаў:
выконваюцца паводле правілаў:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) 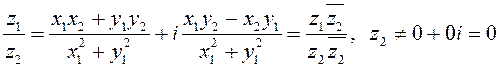 .
.
Геаметрычна кожнаму камплекснаму ліку ![]() адпавядае
пункт М(x; y) каардынатнай плоскасці і, наадварот, кожнаму пункту М(x; y)
плоскасці адпавядае камплексны лік
адпавядае
пункт М(x; y) каардынатнай плоскасці і, наадварот, кожнаму пункту М(x; y)
плоскасці адпавядае камплексны лік ![]() . Гэтую
плоскасць называюць камплекснай плоскасцю, вось абцыс – рэчаіснаю
воссю, а вось ардынат – уяўнай воссю. Часам бывае больш
зручна выяўляць камплексны лік
. Гэтую
плоскасць называюць камплекснай плоскасцю, вось абцыс – рэчаіснаю
воссю, а вось ардынат – уяўнай воссю. Часам бывае больш
зручна выяўляць камплексны лік ![]() як вектар з пачаткам у пункце О і
канцом у пункце M.
як вектар з пачаткам у пункце О і
канцом у пункце M.
Модулем камплекснага ліку z
называецца даўжыня адпаведнага яму вектара. Модуль ліку ![]() абазначаецца |z| і вылічаецца паводле формулы
абазначаецца |z| і вылічаецца паводле формулы
![]() . (1.6)
. (1.6)
Аргументам камплекснага ліку ![]() называецца
вугал паміж дадатным кірункам рэчаіснай восі і вектарам z. Для ліку
называецца
вугал паміж дадатным кірункам рэчаіснай восі і вектарам z. Для ліку ![]() аргумент не
азначаецца. Аргумент камплекнага ліку z
абазначаецца
аргумент не
азначаецца. Аргумент камплекнага ліку z
абазначаецца ![]() і вызначаецца з дакладнасцю да
складніка, кратнага 2π.
і вызначаецца з дакладнасцю да
складніка, кратнага 2π.
З геаметрычных меркаванняў зусім проста падаць
рэчаісную і ўяўную часткі камплекснага ліку ![]() праз
яго модуль r і аргумент
праз
яго модуль r і аргумент ![]() :
:
![]() , (1.7)
, (1.7)
або з улікам роўнасці (1.6)
![]() . (1.8)
. (1.8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.