Вучэбны дапаможнік для студэнтаў фізічнага і радыёфізічнага факультэтаў у пяці частках, страница 4

Аргументы камплекснага ліку  можна вылічыць з раўнання , якое ёсць вынік сістэмы (1.8). Гэтае раўнанне мае больш развязкаў, чым сістэма (1.8), але выбраць патрэбныя развязкі (аргументы камплекснага ліку) можна паводле правіла: калі , (г. зн. лік z размяшчаецца ў правай паўплоскасці), то ; калі Rez<0, (г. зн. лік z размяшчаецца ў левай паўплоскасці), то .

З роўнасцяў (1.7) вынікае, што камплексны лік  можна падаць ў выглядзе , дзе r = |z|, φ = arg z. Такое выяўленне камплекснага ліку называецца трыганаметрычнай формай камплекснага ліку. Трыганаметрычная форма з’яўляецца вельмі зручнай для множання і дзялення камплексных лікаў. Калі  , , то

, .

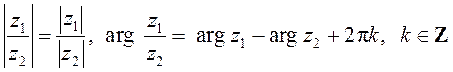На падставе гэтых роўнасцяў выводзіцца формула Муаўра

.

Камплексны лік wназываецца коранем ступені n з камплекнага ліку z і абазначаецца , калі . Калі , то існуе n значэнняў кораня ступені n з ліку z, якія знаходзяцца паводле формулы

.                  (1.9)

Камплексныя лікі, якія ёсць карані ступені n з камплекснага ліку z, адпавядаюць пунктам камплекcнай плоcкасці, размешчаным у вяршынях правільнага n-вугольніка, умежанага ў акружыну радыуса  з цэнтрам у пункце О.

Прыклад 1. Пераўтварыць бясконцыя дзесятковыя перыядычныя дробы a= 3,(17) і b= 2,5(123) у рацыянальныя дробы.

▶ 1. Памножым лік a на 100 і атрымаем 100а = 317,(17). Калі ад абедзвюх частак гэтай роўнасці адняць лік а, то атрымаем 99а = 314, адкуль а = 314/99.

2. Калі абазначыць x= 10b= 25,(123), то, як і ў папярэднім выпадку, лік x пераўтвараецца ў рацыянальны дроб: 1000х = 25123,(123); 999x= 25098, x= 25098/999, а затым b = 25098/9990 ◄

Прыклад 2. Вызначыць аргументы камплексных лікаў  .

▶ Паколькі лік  размяшчаецца ў чацвёртым квадранце, то arg. У той жа час , а таму

arg.  ◄

Прыклад 3. Знайсці модулі і аргументы лікаў

.

▶ Для знаходжання модуляў і аргументаў лікаў  і  зусім неабавязкова карыстацца формуламі (1.6) і (1.8). На падставе формул прывядзення выканаем наступныя пераўтварэнні:

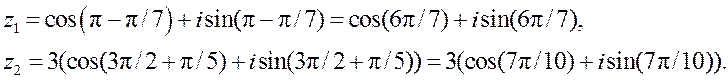Паколькі  і  пададзены ў трыганаметрычнай форме, то , arg z₁=6π/7+2πk, ||=3, arg =7π/10+2πk, . ◄

Прыклад 4. Запісаць у трыганаметрычнай форме камплексны лік

.

▶ Паколькі лік =cos(/12)–isin(/12) мае ||=1 і arg =–π/12, лік = мае || = 4 і arg  = /6, а лiк = мае || = 2 і arg = – /4, то 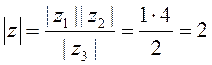,   адкуль z = 2(cos(/3)+isin(/3)). ◄

Прыклад 5. Вылічыць .

▶ Пры вылічэнні кораня квадратовага часам бывае больш зручна выкарыстоўваць замест формулы (1.9) азначэнне кораня другой ступені з камплекснага ліку. Няхай , тады 5–12і = . Лікі а і b знаходзяцца з сістэмы раўнанняў   развязкі якой (–3; 2) і (3; –2). Такім чынам, камплексныя лікі –3 + 2і і 3 – 2і, ёсць два значэнні . ◄

Задачы

1.25.  Параўнайце рэчаісныя лікі а і b: 1) a = 1,(1234512), b = 1,(12345);      2) a = 1,0(123), b = 1,0(1231); 3) a = 1,(01), b = 1,0(101);                  4) a = 1,(1312), b = 1,13(12).

1.26.  Запішыце ў выглядзе бясконцых дзесятковых дробаў рацыянальныя лікі: 1) ;          2) ;         3) ;         4) .

1.27.  Запішыце перыядычныя бясконцыя дзесятковыя дробы ў выглядзе рацыянальных лікаў: 1) 0,125(0);    2) 0,(7); 3) 2,4(31);    4) 0,2(9).

1.28.  Параўнайце рацыянальныя лікі  і :  1) а= 2,(13), b = ; 2) a = 0,0(17), b = ;  3) а= , b = ;  4) а= 0,(139), b = .

1.29.  Знайдзіце суму a + b рэчаісных лікаў:        1) а= 0,(12), b = 0,(13);  2) а= 0,(51), b = 0,(53); 3) а= 0,(7), b = 0,(31);    4) а= 0,1(7), b = 0,(17).

1.30.  Дакажыце, што наступныя лікі ёсць ірацыянальныя: 1) log₂3;  2) lg3;  3) ;  4) .

1.31.  Параўнайце рэчаісныя лікі a i b: 1) а= 2+, b = ;        2) а= , b = ; 3) а= , b = ;  4) а= , b = .

1.32.  Які з лікаў большы:  1) а ці –а;  2) а ці , калі а≠0?

1.33.  Дакажыце, што мноства  ёсць абмежаванае, калі і толькі калі існуе такі лік , што для ўсіх  праўдзіцца няроўнасць .

1.34.  Знайдзіце дакладныя верхнія і ніжнія межы мностваў: 1) {n};        2){ };         3) {};        4) {} ().