Спосаб другі. Вылучаючы
ў суме квадратаў ![]() квадрат сумы,
атрымаем
квадрат сумы,
атрымаем ![]() . Раскладаючы правую частку на множ-нікі як
розніцу квадратаў, прыходзім да таго ж самага выніку.◄
. Раскладаючы правую частку на множ-нікі як
розніцу квадратаў, прыходзім да таго ж самага выніку.◄
2º. Рацыянальнай функцыяй называецца выраз ![]() ,
дзе
,
дзе ![]() – мнагасклады. Калі ступень
мнагаскладу
– мнагасклады. Калі ступень
мнагаскладу ![]() меншая за ступень мнагаскладу
меншая за ступень мнагаскладу ![]() , то рацыянальная функцыя
, то рацыянальная функцыя ![]() называецца правільнай.
У іншым выпадку функцыя
называецца правільнай.
У іншым выпадку функцыя ![]() называецца няправільнай
і яе можна падаць у выглядзе
называецца няправільнай
і яе можна падаць у выглядзе 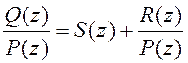 , дзе
, дзе ![]() ёсць дзель, а
ёсць дзель, а ![]() – астача ад дзялення
мнагаскладу
– астача ад дзялення
мнагаскладу ![]() на
на ![]() .
Пры гэтым рацыянальная функцыя
.
Пры гэтым рацыянальная функцыя ![]() ёсць
правільная, або
ёсць
правільная, або ![]() .
.
Няхай ![]() ёсць
правільная рацыянальная функцыя, і
ёсць
правільная рацыянальная функцыя, і ![]() –
мнагасклады з рэчаіснымі каэфіцыентамі, прычым расклад мнагаскладу
–
мнагасклады з рэчаіснымі каэфіцыентамі, прычым расклад мнагаскладу ![]() на множнікі мае выгляд (1.12).
Тады існуюць рэчаісныя канстанты
на множнікі мае выгляд (1.12).
Тады існуюць рэчаісныя канстанты ![]() такія, што
мае месца роўнасць
такія, што
мае месца роўнасць
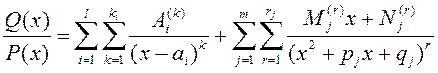 .
(1.13)
.
(1.13)
Складнікі ў правай частцы роўнасці (1.13) называюцца простымі рацыянальнымі дробамі. Асноўныя спосабы знаходжання каэфіцыентаў раскладу правільнай рацыянальнай функцыі на суму простых дробаў разгледзім на прыкладах.
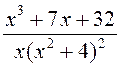 ; 2.
; 2. 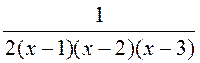 ; 3.
; 3. 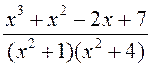 ; 4.
; 4. 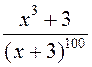 .
.►1. На падставе формулы (1.13) маем:
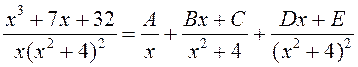 .
.
З роўнасці рацыянальных дробаў вынікае роўнасць
мнагаскладаў ![]() . Прыраўноўваючы каэфіцыенты пры аднолькавых ступенях х,
атрымаем сістэму:
. Прыраўноўваючы каэфіцыенты пры аднолькавых ступенях х,
атрымаем сістэму:
![]()
развязак якой ёсць ![]() .
Такім чынам,
.
Такім чынам,
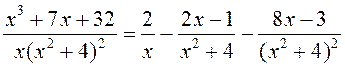 .
.
Гэты спосаб называецца спосабам адпаведных каэфіцыентаў.
2. У выпадку, калі корні назоўніка рацыянальнай функцыі простыя, вельмі зручным з’яўляецца спосаб дамнажэння. Спачатку запішам расклад дробу з нявызначанымі каэфіцыентамі:
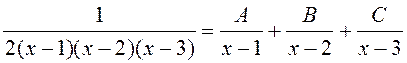 .
.
Дамнажаючы абедзве часткі гэтай роўнасці на ![]() ,
маем
,
маем
 .
.
Надаючы абедзвюм часткам атрыманай роўнасці значэнне ![]() (корань мнагаскладу
(корань мнагаскладу ![]() ), атрымаем
), атрымаем ![]() . Аналагічна вылічаюцца
. Аналагічна вылічаюцца ![]()
![]() .
.
3. Карані назоўніка ў гэтым выпадку таксама простыя, хаця і камп-лексныя. Карыстаемся спосабам дамнажэння:
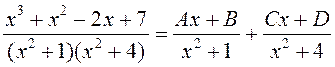 , адкуль
, адкуль ![]() .
.
Беручы значэнні ![]() і
і ![]() , атрымаем
, атрымаем
![]() .
.
З гэтай сістэмы знаходзім ![]() Такім
чынам,
Такім
чынам,
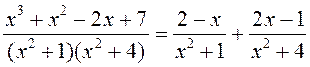 .
.
4. Беручы ![]() ,
атрымаем
,
атрымаем
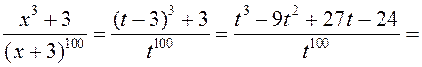
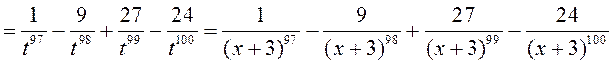 .◄
.◄
1.94. Вызначце канстанты A,B, C,D так, каб праўдзіліся роўнасці:
1) 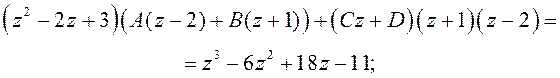 2)
2) ![]() 3)
3) ![]() .
.
1.95.
Знайдзіце дзель ![]() і астачу
і астачу ![]() ад дзялення мнагаскладу
ад дзялення мнагаскладу ![]() на мнагасклад
на мнагасклад ![]() :
1)
:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
1.96.
Ці дзеліцца мнагасклад
![]() на мнагасклад
на мнагасклад ![]() :
1)
:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() ?
?
1.97.
Для якіх значэнняў а
і b мнагасклад ![]() дзеліцца на
дзеліцца на ![]() :
1)
:
1) ![]() 2)
2) ![]() 3)
3) ![]() ?
?
1.98. Пры дзяленні мнагаскладу ![]() на
на ![]() атрымліваецца
астача 7, а пры дзяленні на
атрымліваецца
астача 7, а пры дзяленні на ![]() – астача 3.
Знайдзіце астачу ад дзялення
– астача 3.
Знайдзіце астачу ад дзялення ![]() на
на ![]() .
.
1.99. Пры дзяленні мнагаскладу ![]() на
на ![]() атрымліваецца
астача
атрымліваецца
астача ![]() , а пры дзяленні на
, а пры дзяленні на ![]() – астача
– астача ![]() . Знайдзіце астачу ад дзялення
. Знайдзіце астачу ад дзялення ![]() на
на ![]() .
.
1.100. Дакажыце, што цэлыя карані мнагаскладу з цэлымі каэфіцыентамі ёсць дзельнікі вольнага складніка гэтага мнагаскладу.
1.101.
Знайдзіце цэлыя
карані раўнанняў:
1) ![]() ; 2)
; 2) ![]() 3)
3) ![]() ; 4)
; 4) ![]() .
.
1.102. Дакажыце, што кожны рацыянальны корань мнагаскладу з цэлымі каэфіцыентамі можна падаць у выглядзе p/q, дзе p ёсць дзельнік вольнага складніка, а q – дзельнік найвышэйшага каэфіцыента гэтага мнагаскладу.
1.103.
Знайдзіце
рацыянальныя карані раўнанняў:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
1.104.
Развяжыце раўнанні:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
1.105. Дакажыце, што калі мнагасклад з рэчаіснымі
каэфіцыентамі мае камплексны корань ![]() , то лік
, то лік ![]() таксама ёсць
корань гэтага мнагаскладу.
таксама ёсць
корань гэтага мнагаскладу.
1.106.
Пераканайцеся ў тым,
што лік z0 ёсць развязак раўнання, і знайдзі-це астатнія развязкі:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
1.107.
Вызначце кратнасць
кораня z0 раўнання:
1) ![]() ;
2)
;
2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
1.108.
Знайдзіце суму
каэфіцыентаў мнагаскладаў:
1) ![]() ; 2)
; 2) ![]() .
.
1.109.
Падайце мнагасклад у
выглядзе здабытку двух мнагаскладаў другой ступені з рэчаіснымі каэфіцыентамі:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() .
.
1.110.
Вылучыце цэлую частку
рацыянальных функцый:
1) 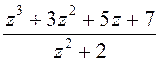 ; 2)
; 2) 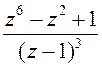 ; 3)
; 3) 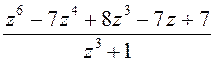 .
.
1.111.
Раскладзіце
рацыянальную функцыю на суму простых дробаў:
1) 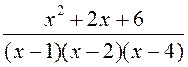 ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) 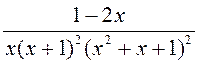 ; 6)
; 6) 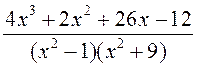 ;
7)
;
7) 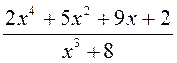 ; 8)
; 8) 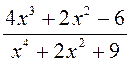 ; 9)
; 9) 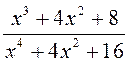 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.