1.35.
Няхай ![]() і
–X=
і
–X=![]() . Дакажыце, што sup(–X) = –inf X,
inf(–X) = –sup X.
. Дакажыце, што sup(–X) = –inf X,
inf(–X) = –sup X.
1.36.
Няхай ![]() ,
,
![]() і
і ![]() ,
,
![]() . Дакажыце, што:
1) sup(X + Y) = supX + supY; 2) inf(X + Y) = infX + infY;
3) sup(X – Y) = supX – infY; 4) inf(X – Y) = infX – supY.
. Дакажыце, што:
1) sup(X + Y) = supX + supY; 2) inf(X + Y) = infX + infY;
3) sup(X – Y) = supX – infY; 4) inf(X – Y) = infX – supY.
1.37.
Дакажыце, што нуль ёсць ніжняя мяжа мностваў:
1) ![]() ; 2)
; 2) 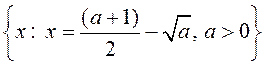 ; 3)
; 3) 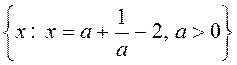 ; 4)
; 4) 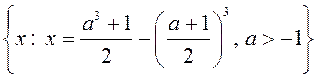 .
.
1.38.
Вызначце рэчаісныя лікі x і y так, каб ![]() :
1)
:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
1.39.
Вылічыце здабытак ![]() і
дзель
і
дзель ![]() , калі:
1)
, калі:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() , 4)
, 4) ![]() .
.
1.40.
Знайдзіце значэнне выразу ![]() , калі:
1)
, калі:
1) ![]() ; 2)
; 2) ![]() .
.
1.41.
Развяжыце сістэму раўнанняў:
1) 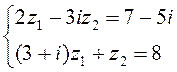 ; 2)
; 2)  .
.
1.42.
На камплекснай плоскасці пункты ![]() ёсць тры
паслядоўныя вяршыні паралелаграма. Знайдзіце чацвёртую вяршыню, калі:
1)
ёсць тры
паслядоўныя вяршыні паралелаграма. Знайдзіце чацвёртую вяршыню, калі:
1) ![]() ; 2)
; 2) ![]()
1.43.
Знайдзіце модуль камплексных лікаў:
1) ![]() ; 2)
; 2) ![]() .
.
1.44.
Дакажыце, што ![]() ёсць
адлегласць паміж пунктамі
ёсць
адлегласць паміж пунктамі ![]() і
і ![]() камплекснай плоскасці.
камплекснай плоскасці.
1.45.
Знайдзіце мноства пунктаў камплекснай
плоскасці, якія задаюцца ўмовамі:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ;
5)
;
5) 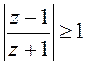 ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() .
.
1.46.
Развяжыце сістэмы раўнанняў: 1) 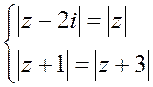 ; 2)
; 2) 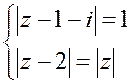 ;
3)
;
3) 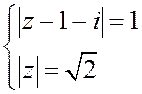 ; 4)
; 4) 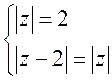 .
.
1.47.
Знайдзіце аргументы камплексных лікаў:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() ;
5)
;
5) ![]() ; 6)
; 6) ![]() ;
7)
;
7) ![]() ; 8)
; 8) ![]() .
.
1.48.
Падайце камплексны лік z у трыганаметрычнай форме:
1) ![]() ; 3)
; 3) ![]() ;
2)
;
2) ![]() ; 4) z=
; 4) z=![]() .
.
1.49.
Запішыце камплексны лік z у алгебраічнай і трыганаметрычнай форме:
1) z = 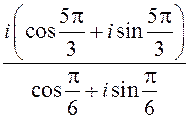 ; 3) z =
; 3) z = 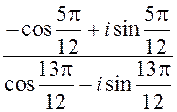 ;
2) z =
;
2) z = 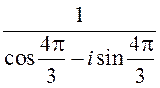 ; 4) z =
; 4) z = 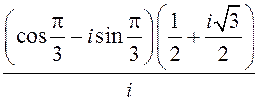 .
.
1.50.
Знайдзіце вектар, у які пераходзіць вектар ![]() пасля павароту на 120°: 1)
у дадатным кірунку; 2) у адмоўным кірунку.
пасля павароту на 120°: 1)
у дадатным кірунку; 2) у адмоўным кірунку.
1.51.
Знайдзіце велічыню вугла, на які трэба
павярнуць вектар ![]() , каб атрымаць вектар,
калі: 1) z1 = 2 – 3
, каб атрымаць вектар,
калі: 1) z1 = 2 – 3![]() + і(3 + 2
+ і(3 + 2![]() ),
), ![]() =4
+6і;
2) z1 = 3
=4
+6і;
2) z1 = 3![]() + i2
+ i2![]() ,
, ![]() =
–5 + і.
=
–5 + і.
1.52.
Запішыце наступныя камплексныя лікі ў алгебраічнай
форме:
1) 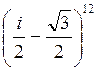 ; 2)
; 2) ![]() ; 3)
; 3) 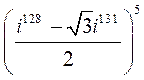 ; 4)
; 4)  ; 5)
; 5) 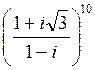 ; 6)
; 6) 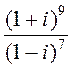 .
.
1.53.
Знайдзіце ўсе значэнні ![]() , калі:
1) z = 8і, n = 3; 2) z = 1, n = 4; 3) z = –1, n = 3; 4) z = 1 + i, n = 2.
, калі:
1) z = 8і, n = 3; 2) z = 1, n = 4; 3) z = –1, n = 3; 4) z = 1 + i, n = 2.
1.54.
Развяжыце раўнанні: 1) ![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
1º. Задачы, звязаныя з выбарам тых або іншых элементаў з некаторага
мноства, называюцца камбінаторнымі. Пры развязанні такіх задач
кіруюцца правілам множання: калі пэўны выбар А можна
зрабіць n рознымі спосабамі, а для кожнага з гэтых
спосабаў іншы выбар В можна ажыццявіць ![]() спосабамі,
то выбар А і В (з названым парадкам) можна зрабіць
спосабамі,
то выбар А і В (з названым парадкам) можна зрабіць ![]() спосабамі.
спосабамі.
Кожнае k элементнае падмноства n– элементнага
мноства называецца спалучэннем з n элементаў
па k элементаў. Колькасць усіх спалучэнняў з n элементаў па k элементаў абазначаецца ![]() і вылічаецца паводле формул
і вылічаецца паводле формул
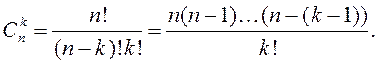 (1.10)
(1.10)
Кожнае ўпарадкаванае k элементнае падмноства n–элементнага мноства
называецца размяшчэннем з n
элементаў па k элементаў. Колькасць усіх размяшчэнняў з n элементаў па k элементаў абазначаецца ![]() і вылічаецца
паводле формул
і вылічаецца
паводле формул 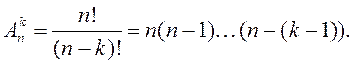
Размяшчэнні з nэлементаў паn элементаў называюцца перастаўленнямі з n элементаў. Колькасць усіх перастаўленняу з n
эле-ментаў абазначаецца ![]() і вылічаецца
паводле формулы
і вылічаецца
паводле формулы ![]() .
.
2º. Разгледзім некаторы дослед з n
роўнамагчымымі зыходамі і падзею А, якая адбываецца, калі дослед
заканчваецца пэўнымі k зыходамі, і не адбываецца ў тым выпадку, калі
мае месца адзін з астатніх n– k
зыходаў. Імавернасцю падзеі А, якая адпавядае доследу з ![]() роўнамагчымымі зыходамі, называецца стасунак
колькасці k зыходаў, спрыяльных падзеі А, да
колькасці ўсіх зыходаў, што абазначаецца
роўнамагчымымі зыходамі, называецца стасунак
колькасці k зыходаў, спрыяльных падзеі А, да
колькасці ўсіх зыходаў, што абазначаецца ![]() .
.
3º. Для рэчаісных лікаў а, b і кожнага ![]() праўдзівая формула бінома Ньютана:
праўдзівая формула бінома Ньютана: 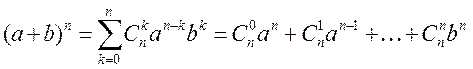 , дзе каэфіцыенты
, дзе каэфіцыенты ![]() называюцца біномнымі
каэфіцыентамі і вылічаюцца паводле формулы (1.10), а
называюцца біномнымі
каэфіцыентамі і вылічаюцца паводле формулы (1.10), а ![]() = 1. Уласцівасць
= 1. Уласцівасць ![]() дае магчымасць выпісаць
біномныя каэфіцыенты ў выглядзе табліцы, якую называюць трохвугольнікам
Паскаля:
дае магчымасць выпісаць
біномныя каэфіцыенты ў выглядзе табліцы, якую называюць трохвугольнікам
Паскаля:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.