Вучэбны дапаможнік для студэнтаў фізічнага і радыёфізічнага факультэтаў у пяці частках, страница 6

1  1

1  2  1

1  3  3  1

1  4   6   4  1

1  5  10  10  5  1

...................

Прыклад 1. Колькі шасцізнакавых лікаў, кратных 5, можна скласці з лічбаў 1, 2, 3, 4, 5, 6 пры ўмове, што ў ліку лічбы не паўтараюцца?

►Паколькі лік дзеліцца на 5, то яго апошняя лічба павінна быць 5. Астатнія 5 лічбаў могуць стаяць на вольных пяці месцах у адвольным па-радку. Таму шуканая колькасць шасцізнакавых лікаў роўная 5! = 120. ◄

Прыклад 2. У партыі з N дэталяў маецца n стандартных. Знайсці імавернасць таго, што з M выпадкова ўзятых дэталяў роўна m будзе стандартных.

►Калі з N дэталяў выбіраць па M дэталяў, то такіх магчымасцяў выбару будзе . Калі сярод выбраных M дэталяў ёсць m стандартных, то нестандартных будзе M – m. Магчымасцяў для выбару m стандартных дэталяў будзе , а для выбару M– m нестандартных – . Усіх выбараў з m стандартных i M– m нестандартных дэталяў паводле правіла множання будзе , а таму імавернасць адпаведнай падзеі роўная . ◄

Задачы

1.55.  Вылічыце: 1) 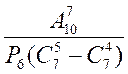; 2) ; 3) .

1.56.  Знайдзіце натуральныя развязкі раўнанняў: 1) ;      2) ;       3) .

1.57.  Колькі пяцізнакавых лікаў дзеляцца на 5?

1.58.  Колькі трохзнакавых лікаў маюць толькі цотныя лічбы?

1.59.  Колькі розных “слоў” можна скласці перастаўленнем літар у словах: 1) доказ;  2) тэарэма;  3) матэматыка?

1.60.  На кніжнай паліцы стаіць збор твораў у 10 тамах. Колькімі спосаба-мі іх можна размясціць, каб:   1) тамы 1 і 2 стаялі побач;    2) тамы 3 і 4 не стаялі побач?

1.61.  З 10 чырвоных і 8 белых ружаў складаецца букет, які змяшчае 2 чырвоныя і 3 белыя ружы. Колькі можна скласці розных букетаў?

1.62.  У калодзе 36 карт, з якіх 4 тузы. Колькімі спосабамі можна раздаць 6 карт, каб: 1) сярод іх не было тузоў; 2) сярод іх было два тузы;                     3) сярод іх быў хаця б адзін туз?

1.63.  У тэнісным турніры удзельнічаюць 6 мужчын і 4 жанчыны. Колькімі спосабамі можна скласці 3 змяшаныя пары?

1.64.  Колькі розных чатырохзнакавых лікаў можна скласці з лічбаў 0, 1, 2, 3, 4, 5, каб: 1) у кожным ліку змяшчалася адна лічба 1;                     2) у кожным ліку змяшчалася хаця б адна лічба 1?

1.65.  Колькі акружынаў можна правесці праз 10 пунктаў плоскасці, з якіх ніякія чатыры не ляжаць на адной акружыне і праз кожныя тры праходзіць адна акружына?

1.66.  На адной з дзвюх паралельных прамых ляжаць 11 пунктаў, на другой – 13. Колькі існуе трохвугольнікаў з вяршынямі ў гэтых пунктах?

1.67.  Колькі дыяганаляў мае выпуклы n– вугольнік?

1.68.  Колькі дзельнікаў мае лік 210?

1.69.  Якая імавернасць таго, што выпадкова выбраны натуральны лік ад 1 да 10 будзе дзельнікам ліку 10?

1.70.  Якая імавернасць таго, што выпадкова выбраны двухзнакавы лік дзеліцца на 3?

1.71.  У скрынцы 3 чырвоных і 9 белых шароў. Якая імавернасць узяць са скрынкі выпадкова чырвоны шар?

1.72.  Манету кідаюць тры разы. Якая імавернасць падзеі, калі: 1) усе тры разы выпалі лічбы; 2) два разы выпалі лічбы і адзін раз герб?

1.73.  Гуляльны кубік кідаецца адзін раз. Знайдзіце імавернасць падзеяў: 1) выпадзенне цотнай колькасці ачкоў; 2) выпадзенне не больш за 5 ачкоў.

1.74.  Гуляльны кубік кідаецца двойчы. Знайдзіце імавернасць таго, што абодва разы выпадзе аднолькавая колькасць ачкоў.

1.75.  Кідаюцца разам два гуляльныя кубікі. Якая імавернасць таго, што: 1) сума ачкоў на абедзвюх гранях роўная 8 ; 2) сума ачкоў на абедзвюх гранях цотная; 3) здабытак ачкоў на абедзвюх гранях роўны 8?

1.76.  Куб з пафарбаванымі ўсімі шасцю гранямі распілаваны на 1000 кубікаў аднолькавага памеру, якія затым старанна перамяшаны. Знайдзіце імавернасць таго, што выпадкова ўзяты кубік будзе мець пафарбаваных граняў:   1) адну:    2) дзве;    3) тры;    4) ніводнай.

1.77.  У скрынцы знаходзіцца 15 дэталяў, з якіх 5 не адпавядаюць стандарту. Знайдзіце імавернасць таго, што тры выпадкова ўзятыя дэталі будуць:   1) стандартнымі;  2) нестандартнымі.