def. Няхай функцыя ![]() вызначана ў акрузе пункта
вызначана ў акрузе пункта ![]() . Калі існуе
. Калі існуе 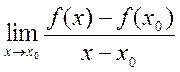 , то гэты ліміт называецца вытворнай функцыі
, то гэты ліміт называецца вытворнай функцыі
![]() у пункце
у пункце ![]() . (У азначэнні нічога
не гаворыцца ні пра існаванне ліміту функцыі, ні пра яе непарыўнасць у пункце
. (У азначэнні нічога
не гаворыцца ні пра існаванне ліміту функцыі, ні пра яе непарыўнасць у пункце ![]() .)
.)
Звычайна вытворную абазначаюць ![]() або
або ![]() паводле Лягранжа,
або
паводле Лягранжа,
або ![]() – паводле Ляйбніца.
Ужываюцца таксама наступныя абазначэнні:
– паводле Ляйбніца.
Ужываюцца таксама наступныя абазначэнні: ![]() –
паводле Ньютана,
–
паводле Ньютана, ![]() – паводле
Кашы.
– паводле
Кашы.
Скарыстоўваючы паняцці прыросту аргументу і прыросту функцыі, атрымліваем:
![]() .
.
► 1) ![]()
![]() ;
;
2) ![]() ,
,
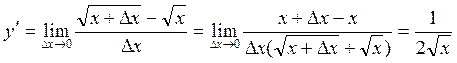 . (Вытворная існуе толькі пры
. (Вытворная існуе толькі пры ![]() , хаця
функцыя
, хаця
функцыя ![]() вызначана і непарыўная пры
вызначана і непарыўная пры ![]() .) ◄
.) ◄
Зазначым, што абазначэнне ![]() азначае
азначае ![]() , а
, а ![]() як вытворная канстанты. Так
для функцыі
як вытворная канстанты. Так
для функцыі ![]() маем
маем 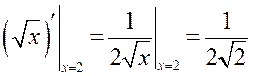 , але
, але ![]() .
.
def. Калі існуюць 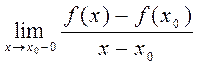 і
і 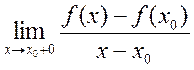 то іх называюць адпаведна левабаковай
і правабаковай вытворнымі функцыі
то іх называюць адпаведна левабаковай
і правабаковай вытворнымі функцыі ![]() у
пункце
у
пункце ![]() і
абазначаюць адпаведна
і
абазначаюць адпаведна ![]() і
і ![]() .
.
З уласцівасцяў лімітаў вынікае: функцыя ![]() мае вытворную ў пункце
мае вытворную ў пункце ![]() , калі і толькі калі яна мае
левабаковую і правабаковую вытворныя:
, калі і толькі калі яна мае
левабаковую і правабаковую вытворныя: ![]() =
=![]() ,прычым
,прычым
![]() =
=![]() =
=![]() .
.![]()
def. Калі функцыя ![]() мае
ў пункце
мае
ў пункце ![]() вытворную, то гэтую функцыю называюць дыферэнцавальнаюў пункце
вытворную, то гэтую функцыю называюць дыферэнцавальнаюў пункце ![]() . З гэтай прычыны аперацыю вылічэння вытворнай функцыі называюць
дыферэнцаваннем.
. З гэтай прычыны аперацыю вылічэння вытворнай функцыі называюць
дыферэнцаваннем.
ڤ Няхай для функцыі ![]() у пункце
у пункце ![]() існуе
вытворная
існуе
вытворная ![]() . З існавання
ліміту вынікае, што
. З існавання
ліміту вынікае, што ![]() =
=![]() , дзе
, дзе ![]() пры
пры ![]() , адкуль
, адкуль ![]() . З апошняй роўнасці
выводзім, што калі
. З апошняй роўнасці
выводзім, што калі ![]() , то
, то ![]() , г.зн. функцыя
, г.зн. функцыя ![]() ёсць непарыўная ў пункце
ёсць непарыўная ў пункце ![]() .■
.■
► ![]()
![]() ,
, ![]()
![]() . Такім чынам,
. Такім чынам, ![]()
![]() , і функцыя
, і функцыя ![]() ёсць недыферэнцавальная ў пункце
ёсць недыферэнцавальная ў пункце ![]() , хаця гэты пункт ёсць пункт
непарыўнасці функцыі
, хаця гэты пункт ёсць пункт
непарыўнасці функцыі ![]() .◄
.◄
![]() (1)
(1)
дзе А
не залежыць ад ![]() . Пры гэтым А=
. Пры гэтым А=![]() і
і
![]() ,
,
або
![]() .
(2)
.
(2)
□ (Неабходнасць) Няхай існуе ![]() , г.зн.
, г.зн. ![]() =
=![]() , адкуль
, адкуль 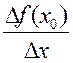 =
=![]() +
+![]() , дзе
, дзе ![]()
![]() пры
пры
![]()
![]() .
Так што
.
Так што ![]() , г. зн. мае месца (2).
, г. зн. мае месца (2).
(Дастатковасць) Калі для функцыі
![]() мае месца выяўленне (1), то
мае месца выяўленне (1), то
![]()
![]() =
=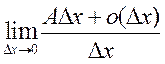 =
=![]()
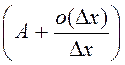 =Α, г. зн.
=Α, г. зн. ![]() ёсць дыферэнцавальная ў пункце
ёсць дыферэнцавальная ў пункце ![]() . ■
. ■
def. Галоўную лінейную частку ![]() прыросту
дыферанцавальнай ў пункце
прыросту
дыферанцавальнай ў пункце ![]() функцыі
функцыі ![]() (гл. (1)) называюць дыферэнцыялам
функцыі і абазначаюць
(гл. (1)) называюць дыферэнцыялам
функцыі і абазначаюць ![]() .
.
Такім чынам,
![]() (3)
(3)
Напрыклад, калі разгледзець функцыю ![]() ,
то
,
то
![]() , г. зн.
, г. зн. ![]() . З гэтай прычыны
звычайна прырост незалежнай зменнай
. З гэтай прычыны
звычайна прырост незалежнай зменнай![]() абазначаюць
абазначаюць
![]() і таму формула (3) набывае
выгляд
і таму формула (3) набывае
выгляд
![]()
Разгледзім геаметрычны сэнс вытворнай і дыферэнцыяла.
Няхай ![]() ёсць
дыферэнцавальная ў пункце
ёсць
дыферэнцавальная ў пункце ![]() функцыя,
а
функцыя,
а ![]() – яе вытворная ў гэтым
пункце. Запішам раўнанне сечнай, што праходзіць праз пункты
– яе вытворная ў гэтым
пункце. Запішам раўнанне сечнай, што праходзіць праз пункты ![]() :
:
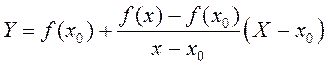 ,
(4)
,
(4)
дзе Х і Y каардынаты пунктаў сечнай.
Калі ў (4) ![]() ,
то вуглавы каэфіцыент сечнай
,
то вуглавы каэфіцыент сечнай 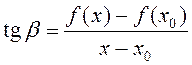 імкнецца
да
імкнецца
да ![]() , г. зн.
, г. зн.
![]() .
(5)
.
(5)
Гэтае раўнанне вызначае лімітавае становішча сечнай, калі ![]() .
.
def. Прамая, да якой імкнецца сечная ![]() , калі
, калі ![]() , называецца датычнай да графіка функцыі
, называецца датычнай да графіка функцыі ![]() ў пункце
ў пункце
![]() .
.
Такім чынам, (5) –ёсць раўнанне датычнай да
графіку функцыі ![]() пункце
пункце ![]() , а вуглавы каэфіцыент
датычнай–
, а вуглавы каэфіцыент
датычнай– ![]() . Гэта значыць, што вытворная
. Гэта значыць, што вытворная
![]() функцыі
функцыі ![]() пункце
пункце![]() ёсць вуглавы каэфіцыент
датычнай да графіка функцыі ў пункце
ёсць вуглавы каэфіцыент
датычнай да графіка функцыі ў пункце ![]() .
.
Адначасова атрымліваем, што дыферэнцыял функцыі ёсць яе прырост па
датычнай. Пры гэтым, чым меншае значэнне мае прырорст незалежнай зменнай ![]() , тым менш адрозніваецца
, тым менш адрозніваецца ![]() ад
ад ![]() , г. зн.
, г. зн. ![]() або
або ![]() . Такім чынам, маем формулу
. Такім чынам, маем формулу
![]() (6)
(6)
для набліжанага вылічэння значэння функцыі праз дыферэнцыял.
► Разгледзім функцыю ![]() . Паколькі
. Паколькі 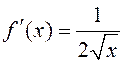 , то, згодна з формулаю (6),
, то, згодна з формулаю (6),
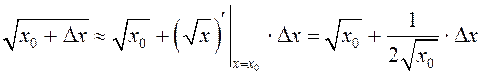 . Калі ўзяць
. Калі ўзяць ![]() , то і атрымаецца формуула
, то і атрымаецца формуула![]() . У прыватнасці
. У прыватнасці
![]()
![]() (як вам падабаецца?);
(як вам падабаецца?);
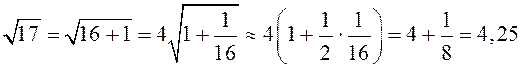 .
.
Зазначым, што даказаная формула ёсць прыватны выпадак атрыманай раней
формулы ![]() . ◄
. ◄
def. Калі функцыя ![]() непарыўная
ў пункце
непарыўная
ў пункце ![]() і
і 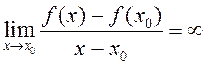 , то кажуць, што функцыя мае
ў пункце
, то кажуць, што функцыя мае
ў пункце ![]() бясконцую вытворную.
бясконцую вытворную.
У гэтам выпадку лімітавае становішча сечнай
пры ![]() вызначаецца раўнаннем
вызначаецца раўнаннем ![]() . Сапраўды, з (1)
атрымліваем
. Сапраўды, з (1)
атрымліваем 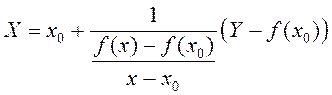 , дзе каэфіцыент
пры
, дзе каэфіцыент
пры ![]() імкнецца да нуля, калі
імкнецца да нуля, калі ![]() , а таму маем
, а таму маем ![]() . У гэтым выпадку датычная
ёсць паралельная восі Oy
. У гэтым выпадку датычная
ёсць паралельная восі Oy


1º. Дыферанцаванне сумы, розніцы, здабытку і дзелі.
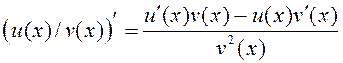 .
.□ Доказ правядзем толькі для дзелі
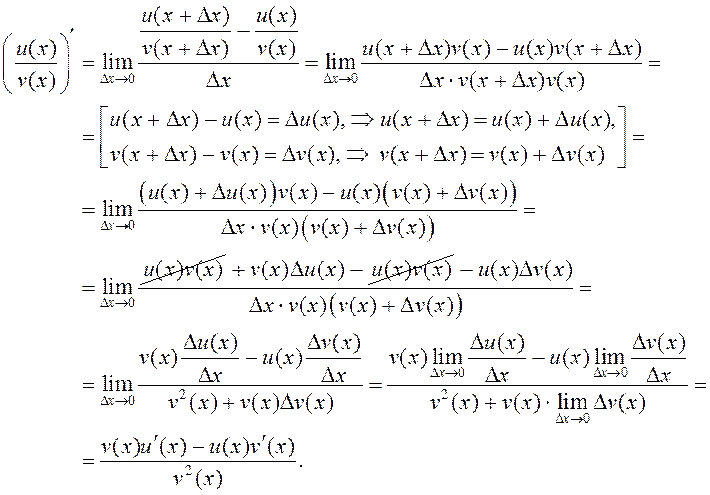 ■
■
2º. Дыферэнцаванне адваротнай функцыі.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.