Дыферэнцыяльнае злічэнне. Вытворная і дыферэнцыял. Адпаведна левабаковай і правабаковай вытворнымі функцыі, страница 5

Заўвага. Тэарэма непраўдзівая на прамежках, якія не з’яўляюцца адрэзкамі. Напрыклад, – непарыўная на (0,1), але неабмежаваная; – непарыўная на , але неабмежаваная.

Другая тэарэма Ваерштраса (пра дасягальнасць дакладных межаў). Калі функцыя f непарыўная на адрэзку , то яна дасягае на гэтым адрэзку сваіх дакладных ніжняй і верхняй межаў, г. зн.

.

□ Згодна з першаю тэарэмаю Ваерштраса функцыя f– абмежаваная на , а таму, на падставе тэарэмы пра межы, існуюць . Пакажам, што існуе .

Дапусцім процілеглае, г. зн. . Паколькі , то , а паколькі , то . Таму функцыя  і непарыўная на. Згодна з першаю тэарэмаю Ваерштраса функцыя g– абмежаваная на , г. зн. 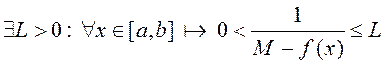. Адкуль маем , а гэта азначае , што  ёсць верхняя мяжа, а таму M – не найменшая з верхніх межаў ?!? Такім чынам, .

Аналагічна даказваецца другая частка тэарэмы. ■

 

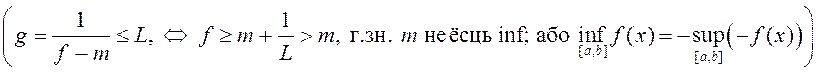
Вынік. Калі функцыя f непарыўная на адрэзку , і , , то мноствам значэнняў функцыі f на адрэзку  з’яўляецца адрэзак . Калі ж m=M, то f(x)=const=m=M. 

Прыклад 1. Функцыя 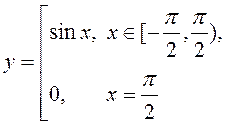 не мае найбольшага значэння на адрэзку , бо разрыўная на гэтым адрэзку.

Калі функцыя f(x) ёсць непарыўная ў пункце , то гэта азначае, што     ( залежыць ад ).

def: Функцыя f(x) называецца раўнамерна непарыўнай на прамежку X , калі

  .

Галоўным у гэтым азначэнні ёсць тое, што няроўнасць  

праўдзіцца адразу  пры адзінай умове .

З раўнамернай непарыўнасці функцыі f на прамежку X вынікае непарыўнасць функцыі у кожным пункце , г. зн. непарыўнасць на X. Адваротнае ж сцверджанне наогул непраўдзівае.

Прыклад 2.

∆ Функцыя непарыўная на (0,1). Пакажам, што яна не з’яўляецца раўнамерна непарыўнаю на гэтым інтэрвале. Дзеля гэтага за-пішам спачатку адмаўленне раўнамернай непарыўнасці функцыі f на прамежку X:

  .

Няхай . Пры гэтым . Маем

.

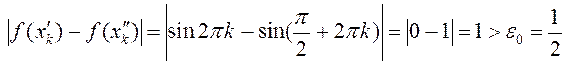Паколькі . то  . Гэта і азначае праўдзівасць умовы нераўнамернай непарыўнасці функцыі. ◄

Тэарэма Кантара. Калі функцыя ёсць непарыўная на адрэзку, то яна раўнамерна непарыўная на гэтым адрэзку.

□ (ад процілеглага) Няхай функцыя f(x) ёсць непарыўная на адрэзку [a,b], але не з’яўляецца раўнамерна непарыўнаю на гэтым адрэзку:

 .

Возьмем адвольную паслядоўнасць: . Для кожнага такога  знойдуцца        .                          (1)

Паколькі  то згодна з прынцыпам выбару з паслядоўнасці  можна вылучыць збежную падпаслядоўнасць . Калі з паслядоўнасці  вылучыць падпаслядоўнасць  з адпаведнымі нумарамі , то атрыманая падпаслядоўнасць  таксама збягаецца да ліміту c, што вынікае з няроўнасцяў . Функцыя f непарыўная на [a,b] і , таму . Але з (1) вынікае, што , адкуль, пераходзячы да ліміту, маем  ?!? ■

Пытанне: Ці можа быць функцыя раўнамерна непарыўнаю на прамежку, які не з’яўляецца адрэзкам, калі яна непарыўная на гэтым прамежку?

Прыклад3.

∆ Возьмем . Разгледзім

, калі . Гэта і азначае раўнамерную непарыўнасць функцыі на інтэрвале (-1,1). ◄

§3.10. Асноўныя тэарэмы пра дыферэнцавальныя функцыі.

def. Няхай існуе –акруга пункта , , ў якой вызначана функцыя  і . Тады кажуць, што функцыя  мае ў пункце  лакальны максімум (мінімум). Лакальны максімум і лакальны мінімум аб’ядноўваюць агульным тэрмінам лакальны экстрэмум.

Тэарэма Фэрма. Калі функцыя  ёсць дыферэнцавальная ў пункце і мае ў пункце  лакальны экстрэмум, то . 

□ Няхай функцыя  мае ў пункце  лакальны максімум. Тады 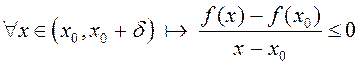 . Адсюль выні-кае, што 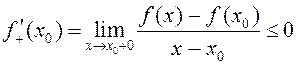. Такім жа чынам  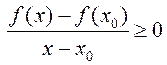, адкуль .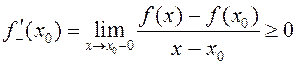

Паколькі функцыя  мае ў пункце  вытворную, то , а таму з атрыманых няроўнасцяў вынікае . Аналагічна разглядаецца выпадак лакальнага мінімума.   ■

Заўвага 1. Функцыя можа не мець вытворную ў пункце , але можа мець лакальны экстрэмум у гэтым пункце. Напрыклад, .

Вынік: Неіснаванне вытворнай і роўнасць яе нулю ёсць неабходная ўмова існавання экстрэмума функцыі ў пункце.

Геаметрычны сэнс тэарэмы Фэрма:

Тэарэма Ролля. Няхай функцыя   ёсць: 1) непарыўная на ; 2) дыферэнцавальная на ; 3) . Тады існуе прынамсі адзін пункт  .