□ Паколькі ![]() ёсць
непарыўная на
ёсць
непарыўная на ![]() , то па другой
тэарэме Ваерштраса яна дасягае на
, то па другой
тэарэме Ваерштраса яна дасягае на ![]() максімальнага
М і мінімальнага m значэнняў.
максімальнага
М і мінімальнага m значэнняў.
Калі ![]() ,
то
,
то ![]() , а таму
, а таму ![]() .
.
Калі ж ![]() ,
то з умовы
,
то з умовы ![]() вынікае,
што функцыя мае прынамсі адно (чаму?) з экстрэмальных значэнняў унутры адрэзка,
г. зн.
вынікае,
што функцыя мае прынамсі адно (чаму?) з экстрэмальных значэнняў унутры адрэзка,
г. зн. ![]() такі, што
такі, што ![]() ёсць экстрэмальнае значэнне
функцыі
ёсць экстрэмальнае значэнне
функцыі ![]() . Паколькі
. Паколькі ![]() – дыферэнцавальная ў с,
то паводле тэарэмы Фэрма
– дыферэнцавальная ў с,
то паводле тэарэмы Фэрма ![]() . ■
. ■
|
Геаметрычны сэнс тэарэмы Ролля: |
|
Прыклад 1. ![]() .
Умовы 1), 2) – выконваюцца, 3)– не мае месца:
.
Умовы 1), 2) – выконваюцца, 3)– не мае месца: ![]() .
.
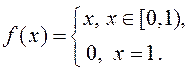 . Умовы 2), 3) –
выконваюцца, 1)– не мае месца:
. Умовы 2), 3) –
выконваюцца, 1)– не мае месца:
Умовы 1), 3) – выконваюцца, 2)– не мае месца:
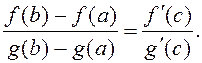
□ Пераканаемся спачатку, што ![]() . Сапраўды, калі б
. Сапраўды, калі б ![]() , то для функцыі
, то для функцыі ![]() былі б выкананымі ўсе ўмовы
тэарэмы Ролля, а таму было б праўдзівым сцверджанне:
былі б выкананымі ўсе ўмовы
тэарэмы Ролля, а таму было б праўдзівым сцверджанне: ![]() . Але гэта супярэчыць умове
тэарэмы.
. Але гэта супярэчыць умове
тэарэмы.
Дзеля далейшага доказу разгледзім дапаможную функцыю ![]() , дзе
, дзе ![]() выберам так, каб
выконвалася ўмова
выберам так, каб
выконвалася ўмова ![]()
![]() ,
г. зн.
,
г. зн.
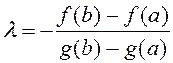 (1)
(1)
Паколькі функцыя ![]() непарыўная
на
непарыўная
на ![]() , дыферэнцавальная на
, дыферэнцавальная на ![]() і
і ![]() , то на падставе тэарэмы
Роля
, то на падставе тэарэмы
Роля ![]() , г. зн.
, г. зн. ![]() , або
, або 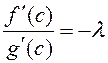 . З улікам (1) маем
. З улікам (1) маем
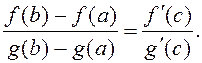 ■
■
.![]() . (2)
. (2)
□ Доказ вынікае непасрэдна з тэарэмы Кашы,
калі ўзяць ![]() . Маем
. Маем ![]() . ■
. ■
|
Геаметрычны сэнс тэарэмы Лягранжа: існуе датычная да графіка функцыі |
|
Няхай ![]() .
Выберам
.
Выберам ![]() так, каб
так, каб ![]() .
.
1) Калі ![]() ,
то да функцыі
,
то да функцыі ![]() , якая адпавядае
на адрэзку
, якая адпавядае
на адрэзку ![]() умовам тэарэмы Лягранжа,
дастасоўваем формулу (2):
умовам тэарэмы Лягранжа,
дастасоўваем формулу (2):
![]() .
(3)
.
(3)
Тут ![]() , г. зн.
, г. зн. ![]() , або
, або ![]() .
.
Калі абазначыць ![]() , то пры
гэтым атрымаем
, то пры
гэтым атрымаем
![]() (4)
(4)
2) Калі ж ![]() , то,
дастасоўваючы на адрэзку
, то,
дастасоўваючы на адрэзку ![]() да
функцыі
да
функцыі ![]() формулу (2), атрымаем
формулу (2), атрымаем ![]() , што раўназначна формуле (3).
Тут
, што раўназначна формуле (3).
Тут ![]() , г. зн.
, г. зн. ![]() , або
, або ![]() . Калі абазначыць, як і
вышэй,
. Калі абазначыць, як і
вышэй, ![]() , то зноў атрымаем роўнасць
(4). Такім чынам, у абодвух выпадках формуле (2) можна надаць наступны выгляд
, то зноў атрымаем роўнасць
(4). Такім чынам, у абодвух выпадках формуле (2) можна надаць наступны выгляд
![]() .
.
Гэтую формулу называюць формулаю Лягранжа канечных прыростаў.
Доказ некаторых няроўнасцяў зручна праводзіць на падставе формулы Лягранжа.
► Разгледзім функцыю ![]() на
адрэзку
на
адрэзку ![]() Паводле тэарэ-мы Лягранжа
Паводле тэарэ-мы Лягранжа ![]() , г. зн.
, г. зн. ![]() .
.
◄
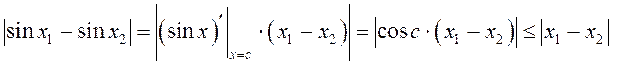 . Такім чынам,
. Такім чынам, Практыкаванне: Даказаць няроўнасць ![]() .
.
□ (Неабходнасць) Калі ![]() , то
, то ![]() .
.
(Дастатковасць) Няхай ![]() . Выберам адвольна
. Выберам адвольна ![]() і на адрэзку
і на адрэзку ![]() да функцыі
да функцыі ![]() дастасуем тэарэму Лягранжа:
дастасуем тэарэму Лягранжа:
![]() . Паколькі
. Паколькі ![]() , то
, то ![]() . ■
. ■
□ Няхай ![]() .
Разгледзім функцыю
.
Разгледзім функцыю ![]() . Адсюль маем
. Адсюль маем![]() . На падставе крытэра сталасці
. На падставе крытэра сталасці
![]() , г. зн.
, г. зн. ![]() . ■
. ■
□ Функцыя ![]() адпавядае
ўмовам тэарэмы Лягранжа на адрэзку
адпавядае
ўмовам тэарэмы Лягранжа на адрэзку ![]() . Таму
. Таму ![]()
![]()
![]() , або
, або
![]() .
(5)
.
(5)
Паколькі ![]() , то
, то ![]() , а таму
, а таму![]() , або
, або
![]() . ■
. ■
Пытанне. Калі ![]() ,
то
,
то ![]() . Ці так гэта?
. Ці так гэта?
► Няхай ![]() .
Пры гэтым
.
Пры гэтым ![]()
![]() .
Паколькі
.
Паколькі ![]() , то
, то ![]() . На падставе тэарэмы пра
дыферэнцыяльную няроўнасць маем
. На падставе тэарэмы пра
дыферэнцыяльную няроўнасць маем ![]() . ◄
. ◄
|
Раней даказалі
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.