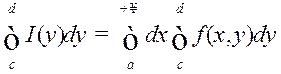Інтэгралы, залежныя ад параметра. Правілам Ляйбніца дыферэнцавання ІЗАП, страница 2

Тэарэма 3 (пра інтэгравальнасць НІЗАП). Калі функцыя  ёсць непарыўная на , а НІЗАП (1) ёсць раўнамерна збежны на , то НІЗАП  ёсць інтэгравальная на  функцыя, прычым 

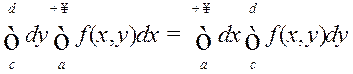, або .         (7)

□ Возьмем адвольнае значэнне  і разгледзім прамавугольнік . Згодна з тэарэмаю 2 §10.1 пра інтэгравальнасць ІЗАП маем

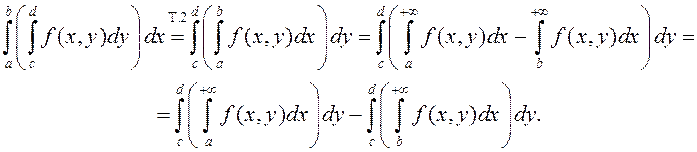        (8)

Калі мы пакажам, што апошні інтэграл у (8) імкнецца да нуля пры , то тым самым дакажам праўдзівасць роўнасці (7). Паколькі НІЗАП (1) ёсць раўнамерна збежны, то

.

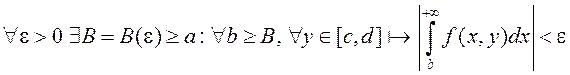Тады 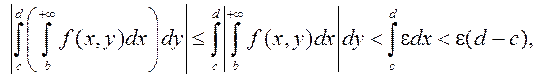 г. зн.

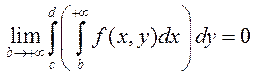.                                           (9)

Калі ў (8) перайсці да ліміту пры , то на падставе (9) атрымаем

, што і азначае праўдзівасць (7). ■

Тэарэма 4 (пра дыферэнцавальнасць НІЗАП). Калі функцыя  і яе частковая вытворная  ёсць непарыўныя на , інтэграл (1) ёсць збежны, а інтэграл 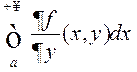 ёсць раўнамерна збежны па  на адрэзку , то НІЗАП  ёсць непарыўна дыферэнцавальная на  функцыя, прычым

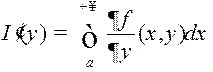                       , г. зн.  (НІЗАП можна дыферэнцаваць па параметру пад знакам інтэграла).

□ Увядзем дапаможную функцыю 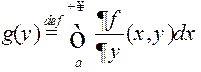. Калі , то функцыя  інтэгравальная на  (тэарэма 3)

Такім чынам, 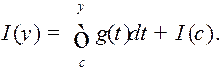 Паводлез тэарэмы Барроў

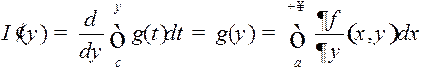, прычым, згодна з тэарэмаю 2, функцыя  ёсць непарыўная на .  ■

§10.3. Інтэграл Дырыхле.

Будзем разглядаць інтэграл 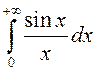, які ёсць збежны на падставе прыкметы Дырыхле: першаісная ад  ёсць абмежаваная, а функцыя  манатонна імкнецца да нуля пры . У пункце  ён існуе як звычайны вызначаны інтэграл. 

Для вылічэння значэння інтэграла Дырыхле разгледзім функцыю

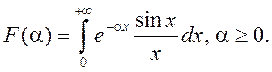                                            (1)

Пакажам, што функцыя  непарыўная пры . Дзеля гэтага спачатку пакажам, што НІЗАП (1) ёсць раўнамерна збежны пры . Вылічым першаісную

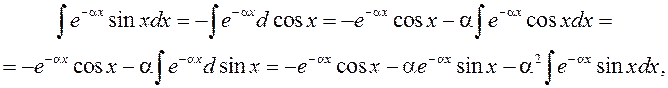
адкуль                                                         (2)

Паколькі  , а

, то

.                                                                  (3)

Карыстаючыся метадам інтэгравання часткамі і няроўнасцю (3), атрымаем

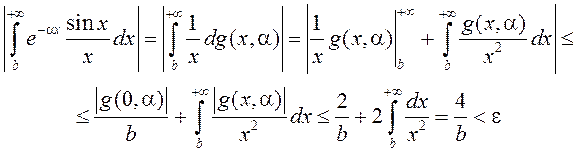
пры  і , што азначае раўнамерную збежнасць НІЗАП (1) пры .

На падставе тэарэмы 2 §10.3 функцыя  непарыўная на .

Дзеля вылічэння вытворнай  разгледзім інтэграл, які атрымліваецца з інтэграла (1) пасля дыферэнцавання яго падынтэгральнай функцыі па параметру

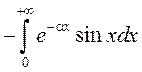                                                              (4)

Гэты інтэграл ёсць раўнамерна збежны на кожным адрэзку , паколькі  і 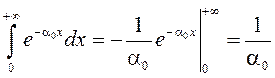 – збежны (прыкмета Ваерштраса). Тады згодна з тэарэмаю 4 §10.2 пры  маем

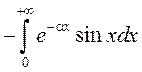
==.                     (5)

Паколькі  і  можна выбіраць адвольна, то роўнасць (5) мае месца пры .

Інтэгруючы (5) па , атрымаем

.                                           (6)

Паколькі 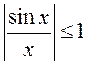 (мы даказвалі, што ), то 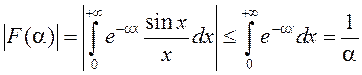. Таму . З роўнасці (6) знойдзем канстанту С:             .

Такім чынам, з (6) маем                               .                                   (7)

На падставе непарыўнасці функцыі  атрымліваем

.

Такім чынам, 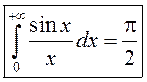   – інтэграл Дырыхле.

З гэтай формулы вынікае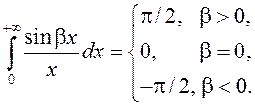    

(Дастаткова ў інтэграле зрабіць замену , або .)

§10.4. Гама – і Бэта – функцыі Ойлера.

Будзем разглядаць так званыя інтэгралы Эйлера, якія па прапанове Ляжандра называюцца таксама Гама – і Бэта – функцыямі.

1º. Гама – функцыя Ойлера. Гэта функцыя уводзіцца як НІЗАП

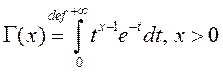                                          (1)

з двума асаблівымі пунктамі  і . Пакажам, што функцыя  непарыўная пры . Дзеля гэтага пададзім (1) у выглядзе сумы двух інтэгралаў:

.

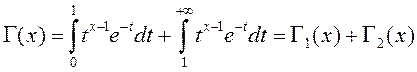Дакажам, што абодва гэтыя інтэгралы ёсць раўнамерна збежныя па параметру  на кожным адрэзку .

1)  Калі  і , то  ( спадальныя, таму найбольшае значэнне на левым канцы). Паколькі інтэграл  ёсць збежны (ён роўны , або пры ), то інтэграл  – раўнамерна збежны на .

2)  Калі ж  і , то  ( нарастальная). Паколькі

 (скарысталіся тым, што ), а інтэграл  – збежны, то інтэграл  ёсць раўнамерна збежны на . Такім чынам, НІЗАП (1) ёсць раўнамерна збежны на , а таму функцыя  – непарыўная на  (тэарэма 2 §10.3), а тым самым  – непарыўная пры .

Аналагічным чынам можна паказаць, што  ёсць непарыўна дыферэнцавальная пры , прычым

 г. зн.  ёсць выпуклая ўніз.

Атрымаем асноўную тоеснасць для .

.

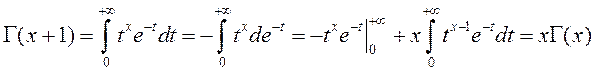Такім чынам,

 –                                     (3)

формула прывядзення для Гама–функцыі. Для вылічэння значэнняў  функцыі  дастаткова ведаць яе значэнні на прамежку .

Паколькі 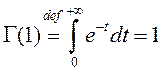, то, беручы ў (3) , атрымаем

.

Вылічым

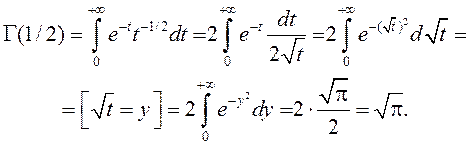
Формула (3) дае магчымасць даследаваць паводзіны функцыі  пры :

.

Улічваючы непарыўнасць , яе выпукласць уніз, яе паводзіны пры  і некаторыя прыватныя значэнні, схематычна нарысуем яе графік

2º. Бэта – функцыя Ойлера. Гэта функцыя уводзіцца як НІЗАП

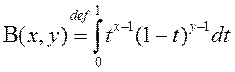                                               (4)

і мае два асаблівыя пункты  і . Запішам (1) у выглядзе

.

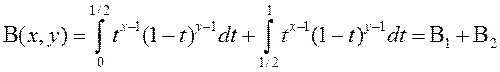Даследуем спачатку інтэграл  на збежнасць у пункце . Паколькі функцыя  ёсць непарыўная пры , то яна абмежаваная, г. зн.

. Тады маем  і паколькі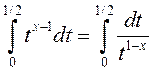

ёсць збежны пры  г. зн. пры , то інтэграл  ёсць збежны (прыкмета параўнання) пры ўсіх  і пры .

Аналагічна паказваецца, што інтэграл  ёсць збежны пры ўсіх  і пры . Такім чынам, функцыя   вызначана пры ўсіх , .

Разгледзім асноўныя ўласцівасці Бэта–функцыі.

1º. Выконваючы ў (1) замену , маем

.

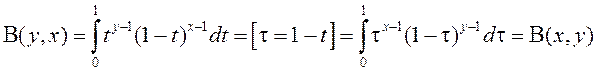2º. Беручы ў (1) 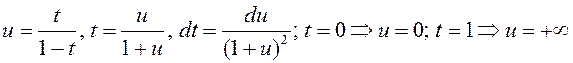, маем

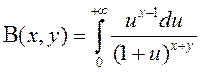 –                                             (5)

другое аналітычнае выяўленне Бэта-функцыі.

Можна паказаць:         

3º.   4º.

Прыклад 1. Выразім інтэграл 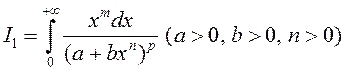 праз Бэта–функцыю.

Зробім замену :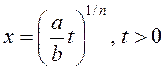

.

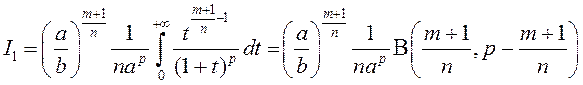Прыклад 2. У інтэграле 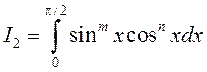 зробім замену

.

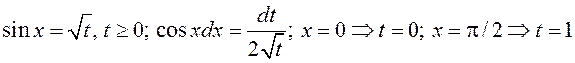
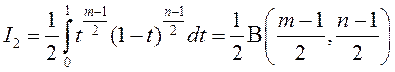Відавочна, што інтэграл ёсць збежны пры