Пабудуем падпаслядоўнасць ![]() лікавай паслядоўнасці
лікавай паслядоўнасці ![]() , якая збягаецца да ліку
, якая збягаецца да ліку ![]() . У якасці
. У якасці ![]() возьмем адвольны элемент
лікавай паслядоўнасці
возьмем адвольны элемент
лікавай паслядоўнасці ![]() . За
. За ![]() возьмем адвольны элемент
паслядоўнасці
возьмем адвольны элемент
паслядоўнасці ![]() з адрэзку
з адрэзку ![]() , для якога
, для якога ![]() (такі выбар магчымы, бо адрэзку
(такі выбар магчымы, бо адрэзку ![]() належыць
бясконца многа элементаў паслядоўнасці
належыць
бясконца многа элементаў паслядоўнасці ![]() ).
У якасці
).
У якасці ![]() возьмем элемент паслядоўнасці
возьмем элемент паслядоўнасці
![]() , які належыць адрэзку
, які належыць адрэзку ![]() і для якога
і для якога ![]() і г.д. Такім чынам, маем
і г.д. Такім чынам, маем
![]() (3)
(3)
Пакажам, што ![]() . Сапраўды, з (2)
і (3) вынікае
. Сапраўды, з (2)
і (3) вынікае
![]()
На падставе прынцыпу двух міліцыянтаў атрымліваем ![]() г.зн.
г.зн. ![]() Гэта і азначае існаванне
збежнай падпаслядоўнасці ў абмежаванай паслядоўнасці. à
Гэта і азначае існаванне
збежнай падпаслядоўнасці ў абмежаванай паслядоўнасці. à
Азначэнне збежнай паслядоўнасці не дае магчымасці даследаваць збежнасці паслядоўнасці, калі мы не ведаем яе ліміту. Таму для нас важна мець “нутраную” прыкмету збежнасці паслядоўнасці (крытэр Кашы), які мы дакажам далей.
def: Лікавая
паслядоўнасць ![]() называецца фундаментальнаю, калі
называецца фундаментальнаю, калі
![]() , або інакш
, або інакш
![]() .
.
Тэарэма 1. (неабходная ўмова фундаментальнасці). Калі лікавая паслядоўнасць фундаментальная, то яна абмежаваная.
□ Няхай ![]() ёсць фундаментальная лікавая паслядоўнасць. Тады мае
месца
ёсць фундаментальная лікавая паслядоўнасць. Тады мае
месца
![]() .
.
Зафіксуем лік ![]() і атрымаем
і атрымаем
![]() .
.
Калі ўзяць ![]() то
то ![]() г.зн.
г.зн. ![]() – абмежаваная лікавая паслядоўнасць. ■
– абмежаваная лікавая паслядоўнасць. ■
Тэарэма2 (Крытэр Кашызбежнасці лікавай паслядоўнасці). Для
таго каб лікавая паслядоўнасць ![]() была збежнаю, неабходна і
дастаткова, каб яна была фундаментальнаю.
была збежнаю, неабходна і
дастаткова, каб яна была фундаментальнаю.
□ Неабходнасць. Няхай ![]() – збежная і лік
– збежная і лік ![]() яе ліміт, г.зн.
яе ліміт, г.зн.
![]()
![]()
![]() .
.
Тады пры ![]() маем
маем
![]()
Згодна з М‑лемаю ![]() – фундаментальная
паслядоўнасць.
– фундаментальная
паслядоўнасць.
Дастатковасць. Няхай ![]() – фундаментальная. На
падставе неабходнай умовы фундаментальнасці яна абмежаваная. Згодна з прынцыпам
выбару з яе можна вылучыць збежную падпаслядоўнасць
– фундаментальная. На
падставе неабходнай умовы фундаментальнасці яна абмежаваная. Згодна з прынцыпам
выбару з яе можна вылучыць збежную падпаслядоўнасць ![]() .
Няхай
.
Няхай ![]() Пакажам, што
Пакажам, што ![]()
Возьмем ![]() З фундаментальнасці
З фундаментальнасці ![]() вынікае, што
вынікае, што ![]()
![]() , а тым самым
, а тым самым ![]() , бо
, бо ![]() .
.
А паколькі ![]() то
то ![]()
Калі ![]() то
то
![]()
гэта значыць ![]() ■
■
Прыклад 1. 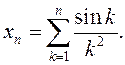
∆ Дакажам, што паслядоўнасць фундаментальная. Разгледзім 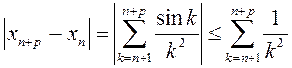 . Улічваючы, што
. Улічваючы, што 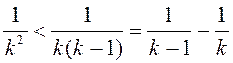 , атрымаем.
, атрымаем.
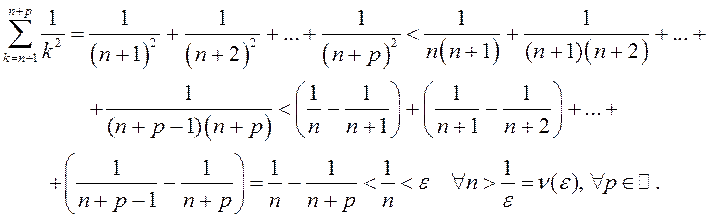
Гэта і азначае, што паслядоўнасць ![]() – фундаментальная, а згодна
з крытэрам Кашы – збежная. ◄
– фундаментальная, а згодна
з крытэрам Кашы – збежная. ◄
Заўвага. Пры гэтым мы даказалі, што шэраг 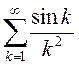 і шэраг
і шэраг ![]() – збежныя (Чаму?).
– збежныя (Чаму?).
Прыклад 2. 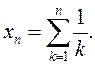
∆ Пакажам, карыстаючыся крытэрам Кашы, што
паслядоўнасць разбежная. Дзеля гэтага запішам адмаўленне фундаментальнасці
лікавай паслядоўнасці: ![]() Возьмем
Возьмем ![]() . Няхай
. Няхай ![]() г.зн.
г.зн. ![]() . Возьмем
. Возьмем ![]() г.зн.
г.зн. ![]() Маем
Маем ![]() Гэта азначае, што паслядоўнасць не
з’яўляецца фундаментальнаю, а, згодна з крытэрам Кашы, гэтая паслядоўнасць
разбежная. Пры гэтым шэраг
Гэта азначае, што паслядоўнасць не
з’яўляецца фундаментальнаю, а, згодна з крытэрам Кашы, гэтая паслядоўнасць
разбежная. Пры гэтым шэраг ![]() , які
называецца гарманічным, таксама разбежны. ◄
, які
называецца гарманічным, таксама разбежны. ◄
def: Калі кожнаму ліку ![]() пастаўлены
ў адпаведнасць паводле некаторага правіла пэўны лік
пастаўлены
ў адпаведнасць паводле некаторага правіла пэўны лік ![]() ,
то кажуць, што на мностве
,
то кажуць, што на мностве ![]() вызначана
лікавая функцыя. Правіла, паводле якога ўсталёўваецца гэтая
адпаведнасць, запісваецца:
вызначана
лікавая функцыя. Правіла, паводле якога ўсталёўваецца гэтая
адпаведнасць, запісваецца: ![]() Пры
гэтым
Пры
гэтым ![]() называецца аргументам
або незалежнай зменнай,
называецца аргументам
або незалежнай зменнай, ![]() –
значэннем функцыі
–
значэннем функцыі ![]() , мноства
, мноства
![]() называюць абсягам
вызначэння функцыі і абазначаюць
называюць абсягам
вызначэння функцыі і абазначаюць ![]() .
Мноства тых лікаў з
.
Мноства тых лікаў з ![]() , кожны з якіх
ёсць значэнне функцыі
, кожны з якіх
ёсць значэнне функцыі ![]() прынамсі для
аднаго значэння
прынамсі для
аднаго значэння ![]() . называюць абсягам
значэнняў функцыі і абазначаюць
. называюць абсягам
значэнняў функцыі і абазначаюць ![]() .
Гэта азначае, што калі
.
Гэта азначае, што калі ![]() , то існуе
прынамсі адно значэнне
, то існуе
прынамсі адно значэнне ![]() Тэрмін функцыя
мае сінонімы адлюстраванне, пераўтварэнне, марфізм.
Тэрмін функцыя
мае сінонімы адлюстраванне, пераўтварэнне, марфізм.
def: Графікамфункцыі ![]() называецца мноства
ўпарадкаваных параў
называецца мноства
ўпарадкаваных параў ![]() Геаметрычнае
выяўленне гэтага мноства таксама называецца графікам.
Геаметрычнае
выяўленне гэтага мноства таксама называецца графікам.
Прыклад 1. ![]() – найбольшы
цэлы лік, які не перавышае
– найбольшы
цэлы лік, які не перавышае ![]() .
.
Прыклад 2. 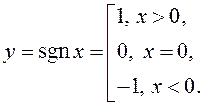
Прыклад 3. ![]()
def: Інтэрвал ![]() называюць ε–акругаюпункта
называюць ε–акругаюпункта ![]() і
абазначаюць
і
абазначаюць
![]() г.зн.
г.зн. ![]() =
=![]() .
.
Калі ε–акругу пазбавіць пункта ![]() ,
то атрыманае мноства называюць праколатаю ε–акругаюпункта
,
то атрыманае мноства называюць праколатаю ε–акругаюпункта ![]() і
абазначаюць
і
абазначаюць ![]()
def: Лік ![]() называюць лімітам
функцыі
называюць лімітам
функцыі ![]() у пункце
у пункце ![]() , калі гэтая функцыя
вызначана ў некаторай праколатай акрузе пункта
, калі гэтая функцыя
вызначана ў некаторай праколатай акрузе пункта ![]() (
у самім пункце
(
у самім пункце ![]() функцыя
можа быць і нявызначанай ) і
функцыя
можа быць і нявызначанай ) і ![]()
![]() , або
, або ![]() .
.
Гэтае азначэнне называюць азначэннем
паводле Кашы або
на мове “![]() ”. Пры гэтым пішуць
”. Пры гэтым пішуць ![]()
 Для функцыі
Для функцыі ![]() маем
маем ![]() . Ці праўда, што
. Ці праўда, што ![]() ?
?
def: Лік ![]() называюць правабаковым(левабаковым)
лімітам функцыі
называюць правабаковым(левабаковым)
лімітам функцыі ![]() у пункце
у пункце
![]() , калі
, калі ![]()
![]() (
(![]() )
) ![]() , што абазначаюць адпаведна
, што абазначаюць адпаведна ![]() (
(![]() ). Пры гэтым кажуць
таксама, што функцыя
). Пры гэтым кажуць
таксама, што функцыя ![]() мае ліміт
мае ліміт ![]() , калі
, калі ![]() імкнецца да
імкнецца да ![]() справа (злева)
справа (злева)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.