Тэорыя лімітаў. Бясконца малыя і бясконца вялікія паслядоўнасці. Збежныя паслядоўнасці, страница 7

Напрыклад, для функцыі Хэвісайда 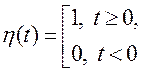 левабаковы і правабаковы ліміты адпаведна роўныя

Пытанне: Ці мае функцыя  ліміт у пункце ? (Не, ліміт існуе толькі тады, калі супадаюць абодва аднабаковыя ліміты.) Менавіта мае месца

Тэарэма 1 ( пра аднабаковыя ліміты). Функцыя  мае ліміт у пункце , калі і толькі калі існуюць правабаковы і левабаковы ліміты ў пункце  і гэтыя ліміты супадаюць, г.зн.  

□ Неабходнасць. Калі для функцыі  існуе , то паводле азначэння аднабаковых лімітаў лік  будзе таксама правабаковым і левабаковым лімітам функцыі  у пункце .

Дастатковасць. Калі існуюць абодва аднабаковыя ліміты і , то паводле азначэння аднабаковых лімітаў

,

.

Калі узяць , то , г.зн. .■

def: Калі функцыя  вызначана ў праколатай акрузе пункта  і , то кажуць, што функцыя  ёсць бясконца вялікая, або мае сваім лімітам  пры , і пішуць . Калі  , то пішуць  ( пры гэтым ). Калі  , то пішуць  ( пры гэтым ).

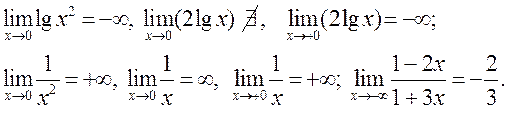def: Калі функцыя  вызначана  і  , то кажуць, што лік  ёсць ліміт функцыі  пры  і пішуць . Калі, то пішуць. Калі, то пішуць.

Напрыклад,

А што азначае ?  ()

Тэарэма 2. (крытэр Гайне існавання ліміту функцыі). Для таго каб функцыя  мела лімітам лік  у пункце , неабходна і дастаткова, каб для кожнай лікавай паслядоўнасці  значэнняў аргумента функцыі ,  адпаведная лікавая паслядоўнасць значэнняў функцыі .

□ Неабходнасць. Няхай , г.зн. , . Возьмем адвольную лікавую паслядоўнасць .  Яе збежнасць азначае, што калі ўзяць выбраны лік  то , а для такіх  выконваецца няроўнась . Гэта і азначае, што .

Дастатковасць. Няхай для кожнай лікавай паслядоўнасці  мае месца .  Дакажам, што .

(ад процілеглага) Дапусцім, што  не ёсць ліміт функцыі  пры . Гэта азначае: . Возьмем адвольную лікавую паслядоўнасць . Пасля гэтага . Мы пабудавалі лікавую паслядоўнасць , якая мае ліміт . Чаму? (Паколькі .) Але пры гэтым . ?!?  ■

Крытэр Гайне дае магчымасць перанесці на паняцце ліміту функцыі ўсе ўласцівасці ліміту лікавай  паслядоўнасці.

Напрыклад, мае месца тэарэма пра адзінасць ліміту функцыі: калі функцыя  мае , то гэты ліміт адзін.

Сапраўды, калі дапусціць, што існуе , то  , але гэта немагчыма на падставе адзінасці ліміту лікавай  паслядоўнасці.

Сфармулюем крытэр Кашы існавання ліміту функцыі, аналагічны крытэру Кашы збежнасці лікавай паслядоўнасці.

Крытэр Кашы (існавання ліміту функцыі). Для існавання ліміту функцыі  у пункце  неабходна і дастаткова, каб   

Тэарэма (пра выяўленне функцыі, якая мае ліміт). Для таго каб функцыя  мела лімітам лік , неабходна і дастаткова, каб                                     .

Маюць месца таксама тэарэмы пра ліміт сумы, розніцы, здабытку і дзелі дзвюх функцый, тэарэма пра лімітавы пераход у няроўнасцях і прынцып сціснутай зменнай. (Сфармуляваць самастойна)

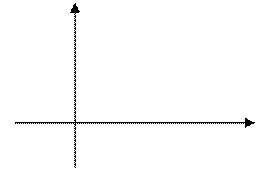
а) правабаковы ліміт. Няхай  З рысунка відаць, што .

Паколькі , то . Усе велічыні ў гэтых няроўна-сцях дадатныя і таму 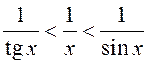.   Далей маем

.

Такім чынам, .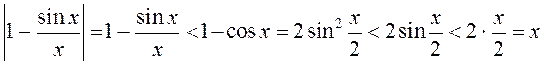

На падставе гэтай няроўнасці атрымліваем

.

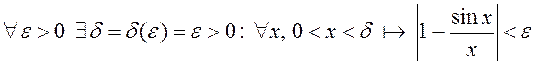Гэта і азначае, што   

б) левабаковы ліміт.   ■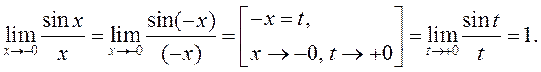

2^о. Грунтоўны ступенева-паказнікавы ліміт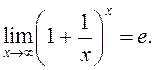  

□ Згодна з крытэрам Гайне мы збіраемся паказаць, што                                                 

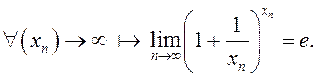
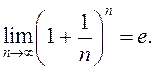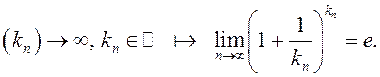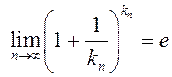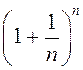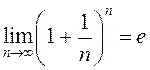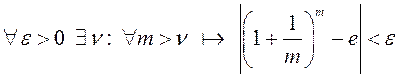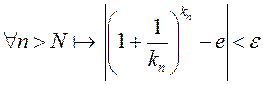Як мы ведаем  Пакажам спачатку, што для кожнай лікавай паслядоўнасці  Калі  нарастальная, то гэта падпаслядоўнасць лікавай паслядоўнасці  і таму  як частковы ліміт лікавай паслядоўнасці . Калі ж  ёсць адвольная, не абавязкова нарастальная, паслядоўнасць натуральных лікаў, то з прычыны таго, што , маем . А паколькі , то для выбранага  . Такім чынам, калі , то , а гэта значыць, што .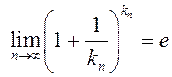

Пакажам далей, што 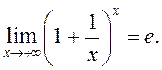 Згодна з крытэрам Гайнэ трэба паказаць, што для кожнай лікавай паслядоўнасці 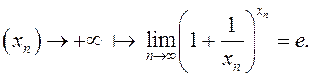 Не парушаючы агульнасці разважанняў, можна лічыць, што  (– бясконца вялікая, а таму пры  ). Возьмем надалей , г.зн.