![]() (1)
(1)
Адкуль
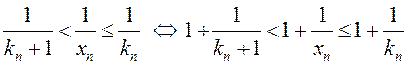 (2)
(2)
З (1) і (2) атрымаем, 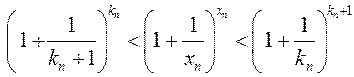 або
або
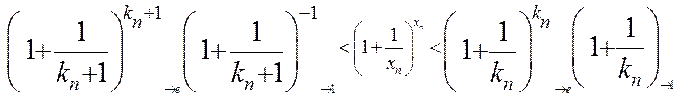 .
.
З тэарэмы пра сціснутую паслядоўнасць вынікае 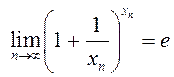 , а на
падставе крытэра Гайне маем
, а на
падставе крытэра Гайне маем 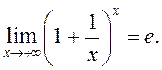
Пакажам далей, што 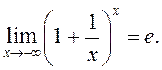 Возьмем
Возьмем ![]() .
Відочна, што
.
Відочна, што ![]() пры
пры
![]() .
Таму
.
Таму 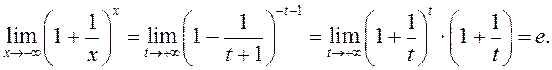 ■
■
Заўвага 1. Калі ўзяць ![]() , то пры
, то пры ![]() . Таму
. Таму
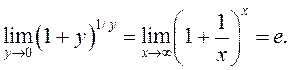
Заўвага 2. Калі ![]() пры
пры ![]() , то і
, то і 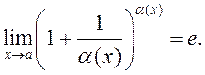
Прыклад. 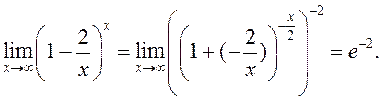
§2.8. Непарыўнасць функцыі. Пункты разрыву.
Пры азначэнні ліміту функцыі fу
пункце ![]() мы
меркавалі, што функцыя ў гэтым пункце можа быць і нявызначанай. Так, да
прыкладу, функцыя
мы
меркавалі, што функцыя ў гэтым пункце можа быць і нявызначанай. Так, да
прыкладу, функцыя ![]() нявызначана
ў пункце
нявызначана
ў пункце ![]() , а
яе ліміт у гэтым пункце роўны 1. Надалей нас будуць цікавіць функцыі,
вызначаныя ў разгляданым пункце.
, а
яе ліміт у гэтым пункце роўны 1. Надалей нас будуць цікавіць функцыі,
вызначаныя ў разгляданым пункце.
def:
Функцыя ![]() называецца
непарыўнаю ў пункце
называецца
непарыўнаю ў пункце ![]() , калі яна
вызначана ў ваколлі гэтага пункта і
, калі яна
вызначана ў ваколлі гэтага пункта і ![]() . Пры
гэтым пункт
. Пры
гэтым пункт ![]() называецца
пунктам непарыўнасці функцыі f . Гэтае
азначае:
называецца
пунктам непарыўнасці функцыі f . Гэтае
азначае:
“на мове ![]() ”:
”:![]()
![]() ,
,
і “на мове паслядоўнасцяў”: ![]()
![]() .
.
def:
Пункт ![]() называецца
ізаляваным пунктам абсягу вызначэння D(f) функцыі
f, калі існуе акруга пункта
называецца
ізаляваным пунктам абсягу вызначэння D(f) функцыі
f, калі існуе акруга пункта ![]() , якая не змяшчае іншых, акрамя
, якая не змяшчае іншых, акрамя ![]() ,
пунктаў абсягу D(f), г.зн.
,
пунктаў абсягу D(f), г.зн. ![]() .
У ізаляваным пункце функцыя лічыцца непарыўнаю.
.
У ізаляваным пункце функцыя лічыцца непарыўнаю.
def:
Розніцу ![]() назавем
прыростам аргумента функцыі ў пункце
назавем
прыростам аргумента функцыі ў пункце ![]() і абазначым яго
і абазначым яго ![]() , а
розніцу
, а
розніцу ![]() назавем
прыростам функцыі, які адпавядае прыросту
назавем
прыростам функцыі, які адпавядае прыросту ![]() і
абазначым яго
і
абазначым яго ![]() .
Такім чынам, маем
.
Такім чынам, маем
![]() .
.
Пры такіх абазначэнных непарыўнасць выражаецца
роўнасцю ![]() , што азначае: малому
прыросту аргумента адпавядае малы прырост функцыі.
, што азначае: малому
прыросту аргумента адпавядае малы прырост функцыі.
def:
Функцыя ![]() называецца непарыўнаю
справа (злева) у пункце
называецца непарыўнаю
справа (злева) у пункце ![]() , калі
, калі ![]()
![]() .
.
З тэарэмы пра аднабаковыя ліміты вынікае, што функцыя
![]() ёсць непарыўная ў пункце,
калі і толькі калі яна непарыўная ў гэтым пункце як злева, так і справа.
ёсць непарыўная ў пункце,
калі і толькі калі яна непарыўная ў гэтым пункце як злева, так і справа.
def: Функцыя называецца непарыўнаю на інтэрвале,
калі яна непарыўная ў кожным пункце гэтага інтэрвала. Функцыя называецца непарыўнаю
на адрэзку ![]() ,
калі яна непарыўная на інтэрвале
,
калі яна непарыўная на інтэрвале ![]() і непарыўная
справа ў пункце
і непарыўная
справа ў пункце ![]() і
злева ў пункце
і
злева ў пункце ![]() .
.
def:
Калі функцыя f вызначана ў праколатай акрузе пункта a , а ў
пункце a функцыя не з’яўляецца непарыўнаю, то пункт a
называецца пунктам разрыву
функцыі f , г.зн. пункт ![]() ёсць
пункт разрыву функцыі
ёсць
пункт разрыву функцыі ![]() ,
калі не выконваецца прынамсі адна з умоваў:
,
калі не выконваецца прынамсі адна з умоваў:
![]() .
.
Прыклады. 1). ![]() пункт
нявызначанасці; 2).
пункт
нявызначанасці; 2). 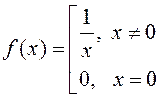 ,
, ![]() – не існуе ліміт. 3).
– не існуе ліміт. 3). ![]() ліміт не роўны
значэнню функцыі ў пункце.
ліміт не роўны
значэнню функцыі ў пункце.
Сярод пунктаў разрыву сустракаюцца некалькі розных выпадкаў.
1º. Функцыя мае ліміт у пункце разрыву.
def:
Пункт разрыву функцыі ![]() называецца
пунктам скасавальнага разрыву, калі ў гэтым пункце функцыя мае ліміт,
г.зн. існуюць абодва аднабаковыя ліміты і
называецца
пунктам скасавальнага разрыву, калі ў гэтым пункце функцыя мае ліміт,
г.зн. існуюць абодва аднабаковыя ліміты і ![]() .
Пры гэтым
.
Пры гэтым ![]() у
пункце скасавальнага разрыву або нявызначана, або
у
пункце скасавальнага разрыву або нявызначана, або ![]() .
.
Напрыклад, Функцыя ![]() мае ў пункце
мае ў пункце ![]() скасавальны
разрыў. Калі ж разгледзець функцыю
скасавальны
разрыў. Калі ж разгледзець функцыю 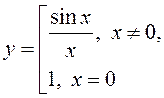 , то яна
непарыўная ў пункце
, то яна
непарыўная ў пункце ![]() ,
г.зн. мы давызначылі функцыю
,
г.зн. мы давызначылі функцыю ![]() у
пункце
у
пункце ![]() па непарыўнасці.
Таму разрыў і называецца скасавальным.
па непарыўнасці.
Таму разрыў і называецца скасавальным.
2º. Функцыя не мае ліміту ў пункце разрыву, але існуюць абодва аднабаковыя ліміты.
def: Калі існуюць абодва аднабаковыя ліміты, але ![]() , то пункт
разрыву
, то пункт
разрыву ![]() называецца
пунктам скачка .
называецца
пунктам скачка .
Напрыклад, пункт ![]() функцыі
Хэвісайда
функцыі
Хэвісайда ![]() ёсць пункт скачка.
ёсць пункт скачка.
def: Пункты скасавальнага разрыву і скачка называюцца пунктамі разрыву першага роду, г.зн. пункты, у якіх існуюць абодва аднабаковыя ліміты.
def: Функцыю, якая мае на мностве ![]() канечную
колькасць разрываў толькі першага роду, называюць кавалкава-непарыўнаю на
мностве
канечную
колькасць разрываў толькі першага роду, называюць кавалкава-непарыўнаю на
мностве ![]() .
.
3º. Не існуе прынамсі адзін з аднабаковых лімітаў.
def: Калі ў пункце разрыву не існуе прынамсі адзін з аднабаковых лімітаў, то пункт разрыву называецца пунктам разрыву другога роду.
Прыклады.
1).Функцыя ![]() пункт
пункт ![]()
 2).
2).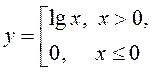 , пункт
, пункт ![]()
![]()
3). 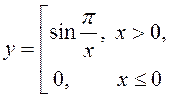 Пакажам, што правабаковы ліміт у пункце 0 не існуе.
Пакажам, што правабаковы ліміт у пункце 0 не існуе.
Дзеля гэтага разгледзім дзве лікавыя
паслядоўнасці ![]()
(тут 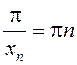 ) і
) і ![]() (тут
(тут 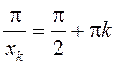 ). Пры гэтым
). Пры гэтым
![]()
Гэта азначае, што 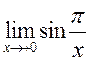 не існуе.
не існуе.![]()
1о. Арыфметычныя дзеянні з непарыўнымі функцыямі.
Калі функцыі ![]() непарыўныя
ў пункце
непарыўныя
ў пункце ![]() , то функцыі
, то функцыі ![]() таксама непарыўныя ў пункце
таксама непарыўныя ў пункце
![]() (у выпадку дзелі пры ўмове
(у выпадку дзелі пры ўмове ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.