Тэорыя лімітаў. Бясконца малыя і бясконца вялікія паслядоўнасці. Збежныя паслядоўнасці, страница 4

Дастатковасць. Доказ правядзем для неспадальнай паслядоўнасці , г.зн. . Паколькі паслядоўнасць ёсць абмежаваная зверху, то  (знізу яна абмежаваная, напрыклад, лікам ). Па тэарэме пра межы лікавая паслядоўнасць  мае дакладную верхнюю мяжу. Няхай . Пакажам, што  ёсць ліміт лікавай паслядоўнасці . Згодна з азначэннем супрэмуму маем

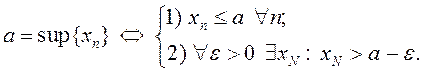
Паколькі паслядаўнасць – неспадальная, то  Такім чынам, , або . Гэта і азначае, што     ■

Пытанне: Дзе скарысталі пры доказе абмежаванасць, а дзе манатоннасць лікавай паслядоўнасці?

Заўвага 1. Тэарэма застаецца праўдзіваю, калі паслядоўнасць ёсць манатонная, пачынаючы толькі з некаторага нумару.

Заўвага 2. Калі лікавая паслядоўнасць  і , то ; калі лікавая паслядоўнасць  і , то . Гэта вынікае з таго, што , .

Прыклад 1. Даследаваць на збежнасць і вылічыць ліміт паслядоўнасці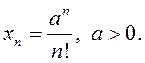

∆ Дакажам, што гэтая лікавая паслядоўнасць – спадальная. Маем

.

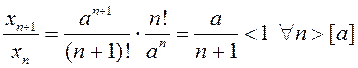Гэта значыць, што паслядоўнасць спадальная пры ўсіх . Пры гэтым яна абмежаваная знізу, бо , а таму збежная. Вылічым яе ліміт. Няхай , пры гэтым . Паколькі , то (Чаму? Як здабытак дзвюх збежных паслядоўнасцяў), што прыводзіць да роўнасці , адкуль маем , або       ◄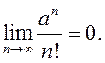

Згодна з азначэннем ліміту паслядоўнасці пры  знойдзецца лік  такі, шт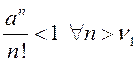о , або  . Такім чынам, мы атрымалі, што

Прыклад 2. Разгледзім лікавую паслядоўнасць , якая задаецца рэкурэнтнаю формулай

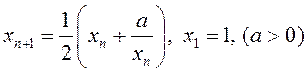.                                      (1)

Паколькі 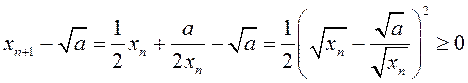, то . Гэта азначае, што палядоўнасць  абмежаваная знізу. Гэта паслядоўнасць ненарастальная, паколькі 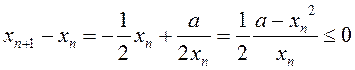 (бо ). Такім чынам, лікавая паслядоўнасць  – збежная. Абазначым . З умовы  вынікае, што . Пераходзячы ў няроўнасці (1) да ліміту, атрымаем раўнанне 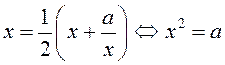, адкуль маем .

Метад вылічэння пры дапамозе рэкурэнтнай формулы называецца метадам ітэрацый. Вылічэнне па формуле (1) выкарыстоўваюць для знаходжання значэння  на кампутарах. Формула (1) дае магчымасць вылічыць значзнне  з любой дакладнасцю.

2°. Лік  як сума шэрагу.

Разгледзім лікавы шэраг . Паслядоўнась яго частковых сумаў 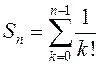 ёсць нарастальная як сума дадатных складнікаў. Пры  маем няроўнасць , з улікам якой атрымліваем

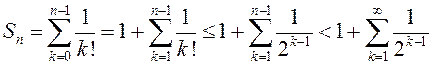.                           (2)

Апошні шэраг у (2) як сума бясконцай геаметрычнай прагрэсіі з назоўнікам  ёсць збежны, а таму паслядоўнасць  абмежаваная зверху. (Чаму? Бо мае месца ацэнка 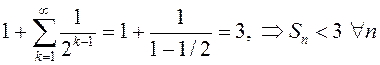)  Такім чынам, паслядоўнасць , як нарастальная і абмежаваная зверху, ёсць збежная, а разам з ёю збежны і шэраг  , сума якога абазначаецца . Такім чынам,.

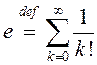.                                                            (3)

З азначэння (3) і няроўнасці (2) маем ацэнку . Ацэнім хібнасць, з якою частковая сума 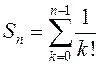 набліжана падае лік . Згодна з (3) маем

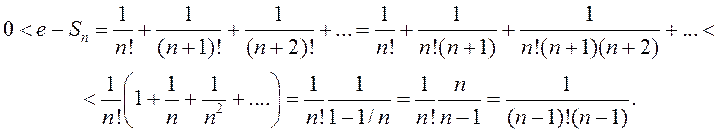
Такім чынам, 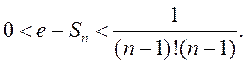                                                                 (4)

Калі , то  г.зн.

Дакажам, што лік  ірацыянальны.

□ Сапраўды (ад процілеглага), няхай 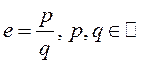, прычым , бо .

У няроўнасці (3) возьмем , атрымаем

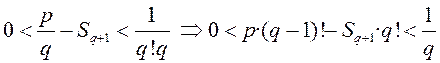, што немагчыма, паколькі лікі  і , а тым самым іх розніца – цэлыя лікі, а лік .  ?1?  Такім чынам, лік  – ірацыянальны.Яго набліжанае значэнне .    à

Як мы пераканаемся пазней, лік  вельмі зручны для выкарыстання ў якасці асновы лагарыфма. Лагарыфмы з такою асноваю называюцца натуральнымі і абазначаюцца .

     def:Функцыю  называюць экспанентаю. Мы будзем таксама часта сустракацца з функцыямі:

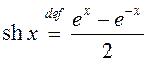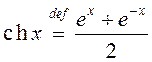 – гіпербалічны сінус і  гіпербалічны косінус.

3°. Лік  як ліміт паслядоўнасці.

Разгледзім лікавую паслядоўнасць 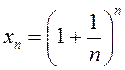 і пакажам, што

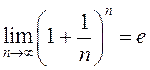.                                                    (5)

□ Карыстаючыся формулаю бінома Ньютана, атрымаем

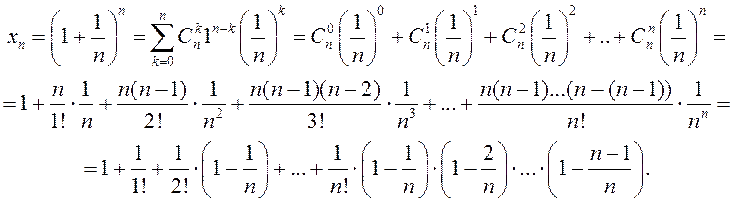    (6)

Калі такім жа чынам распісаць , то атрымаецца на адзін складнік болей, чым у  , і пры гэтым кожны множнік тыпу 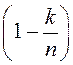 заменіцца на большы 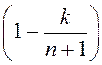. Такім чынам, лікавая паслядоўнасць  – нарастальная.

Паколькі ў (6) усе множнікі тыпу 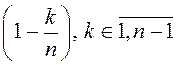 меншыя за адзінку, то

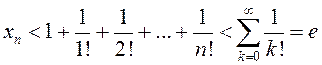, г.зн. лікавая паслядоўнасць  ёсць абмежаваная зверху. Згодна з крытэрам збежнасці манатоннай лікавай паслядоўнасці  – збежная (нарастальная і абмежаваная зверху).