def: Няхай функцыя ![]() вызначаная
на
вызначаная
на ![]() і
строга манатонная на
і
строга манатонная на ![]() ,
г.зн.
,
г.зн. ![]() ,
а тым самым
,
а тым самым ![]() існуе
толькі адзін лік
існуе
толькі адзін лік ![]() такі,
што
такі,
што ![]() .
Такім чынам на мностве
.
Такім чынам на мностве ![]() вызначана
функцыя, якая называецца адваротнаю функцыяй да функцыі
вызначана
функцыя, якая называецца адваротнаю функцыяй да функцыі ![]() і
абазначаецца
і
абазначаецца ![]() .
Відочна, што
.
Відочна, што ![]() ,
а
,
а ![]()
Паколькі ![]() , то графікам
функцый
, то графікам
функцый ![]() і
і
![]() з’яўляецца
адна і тая ж крывая. Але калі адваротную функцыю разглядаць у выглядзе
з’яўляецца
адна і тая ж крывая. Але калі адваротную функцыю разглядаць у выглядзе ![]() , то яе
графік сіметрычны графіку функцыі
, то яе
графік сіметрычны графіку функцыі ![]() у дачыненні да
прамой
у дачыненні да
прамой ![]() .
.
![]()
Тэарэма 3 (пра непарыўнасць адваротнай функцыі). Калі
функцыя ![]() ёсць непарыўная і строга
манатонная на адрэзку
ёсць непарыўная і строга
манатонная на адрэзку ![]() , то вызначаная на
мностве яе значэнняў
, то вызначаная на
мностве яе значэнняў ![]() адваротная да яе
функцыя
адваротная да яе
функцыя ![]() ёсць непарыўная на
ёсць непарыўная на ![]() .
.
□ Няхай ![]() ёсць
нарастальная на
ёсць
нарастальная на ![]() ,
тады
,
тады ![]() На
адрэзку
На
адрэзку ![]() вызначана
функцыя
вызначана
функцыя ![]() ,
прычым, калі
,
прычым, калі ![]() ,
то
,
то ![]() .
Гэта азначае, што функцыя
.
Гэта азначае, што функцыя ![]() ёсць
нарастальная на адрэзку
ёсць
нарастальная на адрэзку ![]() .
Паколькі мноствам яе значэнняў з’яўляецца адрэзак
.
Паколькі мноствам яе значэнняў з’яўляецца адрэзак ![]() , то згодна з
тэарэмаю 2 функцыя
, то згодна з
тэарэмаю 2 функцыя ![]() –
непарыўная на адрэзку
–
непарыўная на адрэзку ![]() .
Аналагічна разглядаецца выпадак спадальнай функцыі. ■
.
Аналагічна разглядаецца выпадак спадальнай функцыі. ■
Нагадаем, што азначае непарыўнасць функцыі ![]() у
пункце
у
пункце ![]() :
:
![]() .
.
1º. Сталая функцыя. Функцыя ![]() ёсць
непарыўная на
ёсць
непарыўная на ![]() .
.
□ Сапраўды, паколькі ![]() , які б
лік
, які б
лік ![]() ні
ўзялі. Гэта і азначае непарыўнасць функцыі ў кожным пункце
ні
ўзялі. Гэта і азначае непарыўнасць функцыі ў кожным пункце ![]() ■
■
2º. Тоесная функцыя. Функцыя ![]() ёсць
непарыўная на
ёсць
непарыўная на ![]() .
.
□ Возьмем адвольны лік ![]() і
няхай
і
няхай ![]() Калі
Калі
![]() ,
то
,
то ![]() .
Гэта і азначае, што
.
Гэта і азначае, што ![]() , або–
непарыўнасць функцыі ў кожным пункце
, або–
непарыўнасць функцыі ў кожным пункце ![]() ■
■
3º.Мнагасклад. Функцыя ![]() -
непарыўная на
-
непарыўная на ![]() .
.
□ Сапраўды ![]() а
мнагасклад ёсць функцыя непарыўная як сума непарыўных функцый
а
мнагасклад ёсць функцыя непарыўная як сума непарыўных функцый ![]() . ■
. ■
4º. Рацыянальная функцыя. Функцыя 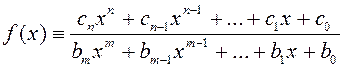 ёсць
непарыўная на
ёсць
непарыўная на ![]() акрамя тых пунктаў, дзе назоўнік роўны
нулю.
акрамя тых пунктаў, дзе назоўнік роўны
нулю.
□ Доказ вынікае з таго, што ліміт дзелі роўны дзелі лімітаў, калі дзельнік не роўны нулю. ■
5º. Трыганаметрычныя функцыі. 1). Функцыя ![]() –
непарыўная на
–
непарыўная на ![]() .
.
□ Спачатку дакажам, што ![]() Калі
Калі ![]() (гл. §2.7.), а таму
(гл. §2.7.), а таму ![]() Калі
Калі ![]() і тады маем
і тады маем ![]() Калі ж
Калі ж ![]() , то з
няроўнасці
, то з
няроўнасці ![]() вынікае,
што
вынікае,
што![]()
Возьмем ![]() ,
маем
,
маем
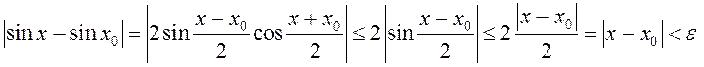 для ўсіх
для ўсіх ![]() , якія
адпавядаюць няроўнасці
, якія
адпавядаюць няроўнасці ![]() Гэта
і азначае непарыўнасць сінуса ў пункце
Гэта
і азначае непарыўнасць сінуса ў пункце ![]() ,
а тым самым і на ўсёй лікавай прамой. ■
,
а тым самым і на ўсёй лікавай прамой. ■
2). Функцыя ![]() –
непарыўная на
–
непарыўная на ![]() .
.
Доказ праводзіцца аналагічна на падставе роўнасці
![]() , або на падставе тэарэмы пра непарыўнасць кампазіцыі і роўнасці
, або на падставе тэарэмы пра непарыўнасць кампазіцыі і роўнасці ![]()
3). Функцыі ![]() –
непарыўныя на.абсягу іх існавання як дзель непарыўных функцый.
–
непарыўныя на.абсягу іх існавання як дзель непарыўных функцый.
6º. Адваротныя трыганаметрычныя функцыі. Функцыі ![]()
![]() непарыўныя на абсягу
іх вызначэння як адваротныя
да непарыўных функцый.
непарыўныя на абсягу
іх вызначэння як адваротныя
да непарыўных функцый.
7º. Экспанента. Функцыя ![]() ёсць
непарыўная на
ёсць
непарыўная на ![]() .
.
□ Спачатку
дакажам, што экспанента непарыўная ў пункце ![]() Дастаткова
даказаць, што
Дастаткова
даказаць, што ![]() , паколькі
, паколькі ![]() Дзеля гэтага
пакажам, што
Дзеля гэтага
пакажам, што ![]() . Пры вылічэнні
правабаковага ліміту ў пункце
. Пры вылічэнні
правабаковага ліміту ў пункце ![]() скарыстаем
крытэр Гайнэ і разгледзім паслядоўнасць
скарыстаем
крытэр Гайнэ і разгледзім паслядоўнасць 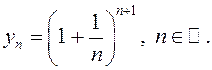 Пераканаемся,
што паслядоўнасць
Пераканаемся,
што паслядоўнасць ![]() ёсць
спадальная. Маем
ёсць
спадальная. Маем
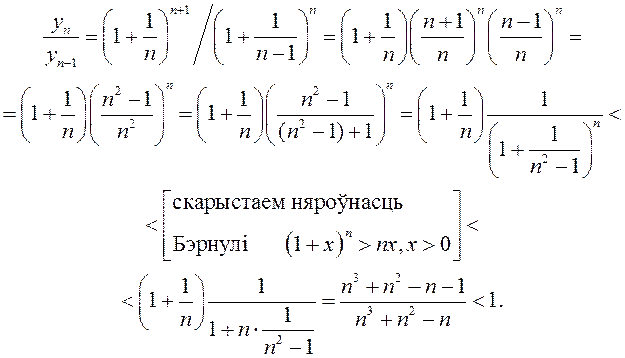
Такім чынам, ![]() , што і азначае
спадальнасць паслядоўнасці
, што і азначае
спадальнасць паслядоўнасці ![]() . Паколькі яе
ліміт
. Паколькі яе
ліміт 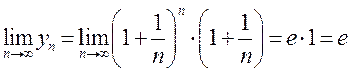 і паслядоўнасць спадальная,
то
і паслядоўнасць спадальная,
то 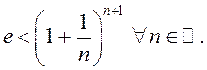 Адсюль
маем
Адсюль
маем 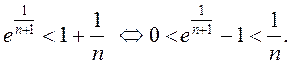 Згодна
з тэарэмаю пра сціснутую зменную
Згодна
з тэарэмаю пра сціснутую зменную ![]() , а тым самым
, а тым самым ![]()
Як і ў выпадку грунтоўнага
ступенева-паказнікавага ліміту ![]()
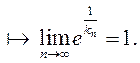 Калі
ўзяць адвольную лікавую паслядоўнасць
Калі
ўзяць адвольную лікавую паслядоўнасць ![]() , то
, то 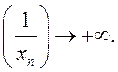 Няхай
Няхай 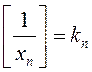 . Маем
. Маем 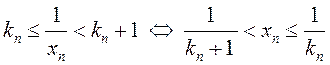 .
Паколькі
.
Паколькі ![]() ,
то
,
то ![]() З
апошняй няроўнасці на падставе тэарэмы пра сціснутую зменную з улікам
З
апошняй няроўнасці на падставе тэарэмы пра сціснутую зменную з улікам 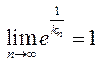 атрымліваем
атрымліваем
![]() .
Згодна з крытэрам Гайнэ маем
.
Згодна з крытэрам Гайнэ маем ![]()
Калі ![]() , то
, то ![]() Такім
чынам,
Такім
чынам, ![]() Тым
самым мы даказалі непарыўнась экспаненты ў пункце
Тым
самым мы даказалі непарыўнась экспаненты ў пункце ![]() .
.
Возьмем ![]() . Маем
. Маем ![]() , паколькі
, паколькі ![]() (?). Такім чынам,
(?). Такім чынам, ![]() , што і
азначае непарыўнасць экспаненты на ўсёй лікавай прамой. ■
, што і
азначае непарыўнасць экспаненты на ўсёй лікавай прамой. ■
8º. Лагарыфмічная функцыя. Функцыя ![]() ёсць
непарыўная на
ёсць
непарыўная на ![]() як адваротная да непарыўнай функцыі
як адваротная да непарыўнай функцыі ![]() . Функцыя
. Функцыя ![]() непарыўная на
непарыўная на ![]()
![]() , паколькі
, паколькі
![]() .
.
9º. Ступеневая функцыя. Функцыя ![]() ёсць
непарыўная на
ёсць
непарыўная на ![]() як кампазіцыя непарыўных функцый
як кампазіцыя непарыўных функцый ![]() (
(![]() ).
).
10º. Паказнікавая функцыя. Функцыя ![]() ёсць
непарыўная на
ёсць
непарыўная на ![]() як кампазіцыя непарыўных функцый
як кампазіцыя непарыўных функцый ![]() . (
. (![]() )
)
11º. Гіпербалічныя функцыі. Функцыі 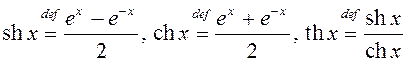 ёсць
непарыўныя на
ёсць
непарыўныя на ![]() ,функцыя
,функцыя ![]() – пры
– пры ![]() як кампазіцыі непарыўных функцый, і называюцца
адпаведна гіпербалічнымі сінусам, косінусам, тангенсам і
катангенсам.
як кампазіцыі непарыўных функцый, і называюцца
адпаведна гіпербалічнымі сінусам, косінусам, тангенсам і
катангенсам.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.