Тэорыя лімітаў. Бясконца малыя і бясконца вялікія паслядоўнасці. Збежныя паслядоўнасці, страница 9

Доказ вынікае непасрэдна з азначэння непарыўнасці і адпаведных ўласцівасцяў лімітаў функцыі.

2^о. Лакальная абмежаванасць непарыўнай функцыі.

def: Функцыя  называецца абмежаванаю зверху (знізу) на мностве , калі называюцца адпаведна верхняй і ніжняй межамі функцыі  на мностве . Функцыя, абмежаваная зверху і знізу на мностве , называецца абмежаванаю на гэтым мностве, г.зн.  

Тэарэма 1. Калі функцыя  вызначана ў ваколлі пункта  і непарыўная ў пункце , то існуе акруга пункта , у якой   ёсць абмежаваная.

□ Непарыўнасць функцыі  у пункце  азначае:   . Зафіксуем , маем

,

г.зн.  – абмежаваная на .  ■

3^о. Стабілізацыя знаку непарыўнай функцыі.

Тэарэма 2. Калі функцыя  вызначана ў ваколлі пункта , непарыўная ў пункце  і , то існуе акруга пункта , у якой знак функцыі  супа-дае з яе знакам у пункце , г.зн.   .

□ Няхай для пэўнасці . З прычыны непарыўнасці  у пункце  для    , адкуль вынікае, што . Выпадак  разглядаецца аналагічна (выбіраецца  )   ■

4^о. Непарыўнасць складанай функцыі.

def: Няхай функцыя  вызначана на , а функцыя  вызначана на , прычым . Тады функцыю, якая  набывае значэнне , называюць складанай функцыяй (або кампазіцыяй, або суперпазіцыяй) функцый  і абазначаюць .   

Тэарэма 3. Калі функцыя  непарыўная ў пункце , прычым , а функцыя  непарыўная ў пункце , то складаная функцыя  непарыўная ў пункце .    

□ Паколькі функцыя  ёсць непарыўная ў пункце , то    

                                                   (1)

мае месца

.                                                   (2)

З непарыўнасці функцыі  ў пункце  маем:  для знойдзенага  існуе  

                                                      (3)

выконваецца няроўнасць

 .                                                    (4)

Калі ў (4) і (2) узяць  і , то з (3) і (2) на падставе (1), (4) маем: . Гэта і азначае, што  – непарыўная ў пункце .   ■

Заўвага. На падставе непарыўнасці складанай функцыі мае месца роўнасць . А паколькі  таксама непарыўная ў пункце , то . З абедзвюх роўнасцяў вынікае

.

Гэта азначае, што для непарыўнай функцыі аперацыя лімітавага пераходу перастаўляльная з аперацыяй дзеяння функцыі.

§2.10. Манатонныя функцыі.

def: Функцыю  называюць нарастальнай на мностве , калі ; неспадальнай, калі ; спадальнай, калі ; ненарастальнай, калі . Усе такія функцыі называюцца манатоннымі. Нарастальныя і спадальныя функцыі называюцца строга манатоннымі.

Тэарэма1. (пра аднабаковыя ліміты манатоннай функцыі). Калі функцыя  вызначаная і манатонная на інтэрвале , то на гэтым інтэрвале яна можа мець пункты разрыву толькі першага роду, г.зн. у кожным пункце  існуюць аднабаковыя ліміты, прычым  (), калі функцыя  ёсць неспадальная (ненарастальная). 

□ Няхай  ёсць неспадальная на . Возьмем адвольны  і разгледзім мноства . Мноства  абмежаванае зверху, паколькі  (функцыя неспадальная). Згодна з тэарэмаю пра межы існуе  . Пры гэтым

                                                              (1)

(бо – верхняя мяжа, а  –найменшая з іх).

Пакажам, што .  Сапраўды,

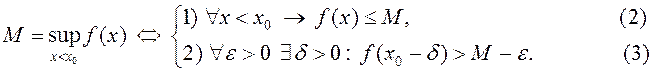
Паколькі  – неспадальная, то

                                      (4)

Такім чынам, маем . Гэта значыць, што , што азначае  а тым самым  Аналагічна даказваецца, што існуе      ■

Тэарэма2. (пра непарыўнасць манатоннай функцыі). Калі функцыя  ёсць манатонная на адрэзку  і мноства яе значэнняў ёсць адрэзак, то яна непарыўная на адрэзку .

□ (ад процілеглага) Няхай  ёсць разрыўная на  і няхай  – яе пункт разрыву (для большай зручнасці разглядаем выпадак пункта разрыву ўнутры адрэзка). Для пэўнасці няхай  ёсць неспадальная. Тады згодна з тэарэмай 1 або , або. Няхай . Паколькі  неспадальная, то  (лімітавы пераход ў няроўнасці), а для . Гэта азначае, што  не набывае значэнняў з інтэрвала  , г.зн. мноства значэнняў функцыі  не ёсць адрэзак.

Аналагічна, калі , то  не набывае значэнняў з інтэрвала .  У абодвух выпадках мноства значэнняў функцыі не ёсць адрэзак. ?!? (Калі ж  то разглядаецца толькі адпаведны аднабаковы ліміт.)  ■