





































Няхай функцыя ![]() вызначана ў некаторым ваколлi пункта
вызначана ў некаторым ваколлi пункта ![]() . Вытворнай функцыi
. Вытворнай функцыi ![]() у пункце
у пункце ![]() называецца лiк
называецца лiк
![]() , (3.1)
, (3.1)
калi ён iснуе. Калi ў роўнасцi (3.1) ![]() , то вытворная называецца правай i
абазначаецца
, то вытворная называецца правай i
абазначаецца ![]() , калi
, калi ![]() , то вытворная называецца левай i
абазначаецца адпаведна
, то вытворная называецца левай i
абазначаецца адпаведна ![]() .
.
ТАБЛIЦА ВЫТВОРНЫХ
1. ![]() ; 2.
; 2. ![]() ; 3.
; 3. ![]() ;
;
4. ![]() ; 5.
; 5. ![]() 6.
6. ![]() ;
;
7. ![]() ; 8.
; 8. ![]() ; 9.
; 9.![]() ;
;
10. 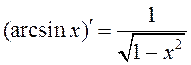 ; 11.
; 11. 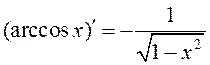 ; 12.
; 12. ![]() ;
;
13. ![]() ; 14.
; 14. ![]() ; 15.
; 15. ![]() ;
;
16. ![]() ; 17.
; 17. ![]() .
.
ПРАВIЛЫ ДЫФЕРЭНЦАВАННЯ
1º. Калi ![]() i
i ![]() маюць вытворныя ў пункце
маюць вытворныя ў пункце![]() , то ў гэтым пункце праўдзяцца роўнасцi :
, то ў гэтым пункце праўдзяцца роўнасцi :
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
2º. Калi функцыя ![]() мае ў пункце
мае ў пункце ![]() вытворную
вытворную ![]() , а функцыя
, а функцыя ![]() мае ў пункце
мае ў пункце ![]() вытворную
вытворную ![]() , то складаная функцыя (альбо кампазiцыя функцый)
, то складаная функцыя (альбо кампазiцыя функцый) ![]() мае вытворную ў пункце
мае вытворную ў пункце ![]() , пры гэтым
, пры гэтым ![]() .
.
3º.
Няхай функцыi ![]() i
i ![]() вызначаны ў некаторым ваколлi пункта
вызначаны ў некаторым ваколлi пункта ![]() i параметрычна задаюць у
ваколлi пункта
i параметрычна задаюць у
ваколлi пункта ![]() функцыю
функцыю ![]() . Калi
. Калi ![]() i
i ![]() маюць у пункце
маюць у пункце ![]() вытворныя і калі
вытворныя і калі ![]() , то функцыя у пункце
, то функцыя у пункце ![]() таксама мае вытворную, якую можна знайсці паводле
формулы
таксама мае вытворную, якую можна знайсці паводле
формулы
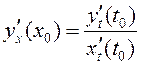 .
(3.2)
.
(3.2)
Прыклад 1. З дапамогай азначэння знайсці вытворную функцыі ![]() .
.
► 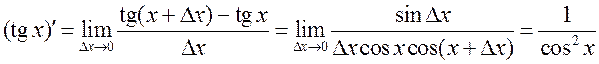 (пры вылічэнні ліміту выкарыстоўвалі формулу
розніцы тангенсаў і грунтоў-ны ліміт
(пры вылічэнні ліміту выкарыстоўвалі формулу
розніцы тангенсаў і грунтоў-ны ліміт ![]() ).◄
).◄
Прыклад 2. Знайсці вытворную функцыі ![]() , карыста-ючыся правілам вылічэння вытворнай
складанай функцыі.
, карыста-ючыся правілам вылічэння вытворнай
складанай функцыі.
►Спачатку пададзім функцыю ![]() у выглядзе кампазіцыі элементарных функцый:
у выглядзе кампазіцыі элементарных функцый: ![]() ;
; ![]() ;
; ![]() . Цяпер
на пад-ставе правіла вылічэння вытворнай складанай функцыі і табліцы вытвор-ных
атрымліваем:
. Цяпер
на пад-ставе правіла вылічэння вытворнай складанай функцыі і табліцы вытвор-ных
атрымліваем:
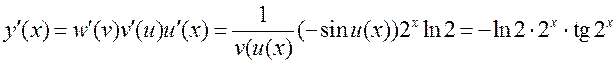 .
.
Заўважым, што вытворная вылічаецца ў адваротным парадку ў параў-нанні з тым, у якім вылічаецца значэнне самой функцыі. ◄
Прыклад 3. Знайсці вытворную ступенева-паказнікавай функцыі
![]()
![]() . (3.3)
. (3.3)
►Першы спосаб. Пададзім функцыю як паказнікавую: ![]() . Тады на падставе правіла дыферэнцавання
складанай функцыі маем
. Тады на падставе правіла дыферэнцавання
складанай функцыі маем
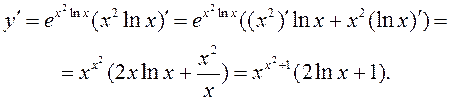
Другі спосаб. Пралагарыфмуем роўнасць (3.3). Атрымаем
![]() . (3.4)
. (3.4)
Цяпер знойдзем вытворныя ад абедзвюх частак роўнасці (3.4):
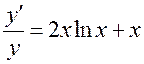 .
.
З апошняй роўнасці і
знаходзім ![]() .◄
.◄
З а ў в а г а.
Для функцыі ![]() вытворная
вытворная ![]() называецца лагарыфмічнай вытворнай.
называецца лагарыфмічнай вытворнай.
Прыклад 4. Вылічыць ![]() для функцыі, зададзенай у палярных
каар-дынатах раўнаннем
для функцыі, зададзенай у палярных
каар-дынатах раўнаннем ![]() ,
, ![]() , у пункце
, у пункце ![]() .
.
►Запішам гэтую функцыю ў
параметрычным выглядзе, калі лічыць параметрам палярны вугал ![]() . Маючы на ўвазе, што палярныя і дэкар-тавыя
каардынаты звязаны паміж сабой формуламі
. Маючы на ўвазе, што палярныя і дэкар-тавыя
каардынаты звязаны паміж сабой формуламі ![]() ,
, ![]() , атрымліваем
, атрымліваем ![]() . Цяпер
вытворная знаходзіцца паводле формулы (3.2):
. Цяпер
вытворная знаходзіцца паводле формулы (3.2):

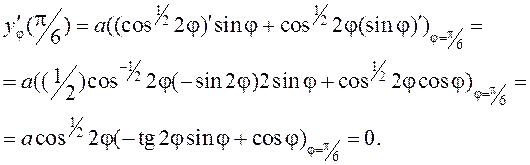
Такім чынам, 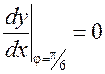 .◄
.◄
3.1.
Карыстаючыся азначэннем, знайдзіце
вытворныя наступных функ-цый:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
3.2.
Вылічыце вытворныя
наступных функцый:
1) 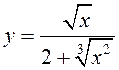 ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ; 10)
; 10) ![]() ; 11)
; 11) ![]() ; 12)
; 12) ![]() ; 13)
; 13) 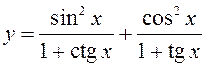 ; 14)
; 14) ![]() 15)
15) 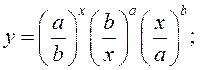 16)
16) ![]() ; 17)
; 17) ![]() ; 18)
; 18) 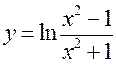 ; 19)
; 19) ![]() ; 20)
; 20) ![]() ; 21)
; 21) ![]() ; 22)
; 22) ![]() ; 23)
; 23) ![]() ; 24)
; 24) ![]() ; 25)
; 25) ![]() ,
, ![]() ; 26)
; 26) ![]() ,
, ![]() ; 27)
; 27) ![]() ,
,![]() ,
, ![]() ; 28)
; 28) ![]() ,
, ![]() ; 29)
; 29) ![]() ; 30)
; 30) ![]() ; 31)
; 31) 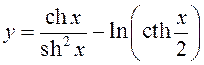 ; 32)
; 32) ![]() ; 33)
; 33) ![]() .
.
3.3.
Знайдзіце вытворныя і
нарысуйце графікі функцый і іх вытворных, калі: 1) ![]() ; 2)
; 2) ![]() .
.
3.4.
Няхай ![]()
![]() , а функцыя
, а функцыя ![]() непарыўная ў некаторым ваколлі пункта
непарыўная ў некаторым ваколлі пункта ![]() . Знайдзіце
. Знайдзіце ![]() .
.
3.5.
Знайдзіце вытворную
функцыі ![]() у пункце
у пункце ![]() , калі: 1)
, калі: 1) ![]() ,
, ![]() =0; 2)
=0; 2)![]() ,
, ![]() =0; 3)
=0; 3)![]() ,
, ![]() =1;
4)
=1;
4)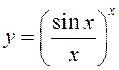 ,
, ![]() =
=![]() .
.
3.6.
Знайдзіце левую ![]() і правую
і правую ![]() вытворныя функцыі
вытворныя функцыі ![]() у пункце
у пункце ![]() , калі:
1)
, калі:
1) ![]() ,
, ![]() =2; 2)
=2; 2) ![]() ,
, ![]() =1; 3)
=1; 3) ![]() ,
, ![]() =0 ; 4)
=0 ; 4) ![]() ,
, ![]() = –1;
5)
= –1;
5) 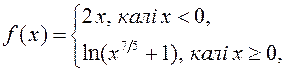
![]() ;
6)
;
6) 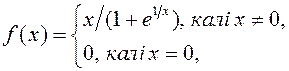
![]() .
.
3.7.
Даследуйце, ці будзе
функцыя ![]() ў пункце
ў пункце ![]() :
а) непарыўнай; б) дыферэнцавальнай, калі:
1)
:
а) непарыўнай; б) дыферэнцавальнай, калі:
1) ![]()
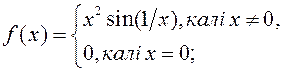 2)
2) ![]()
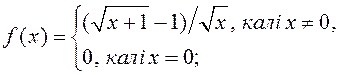 3)
3) ![]()
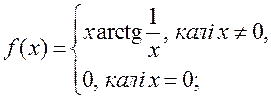 4)
4) ![]() ,
, 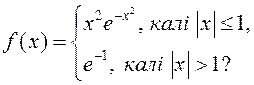
3.8.
Вызначыце, пры якіх
значэннях ![]() і
і ![]() наступныя функцыі будуць а) скрозь
непарыўныя; б) скрозь дыферэнцавальныя. Для гэтых зна-чэнняў
наступныя функцыі будуць а) скрозь
непарыўныя; б) скрозь дыферэнцавальныя. Для гэтых зна-чэнняў ![]() і
і ![]() знайдзіце вытворныя зададзеных функцый:
1)
знайдзіце вытворныя зададзеных функцый:
1) 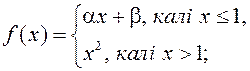 2)
2) 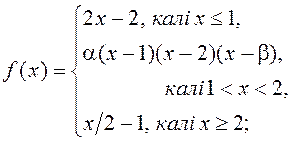 3)
3) 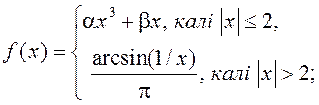 4)
4)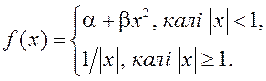 .
.
3.9.
Пры якіх значэннях ![]() функцыя
функцыя 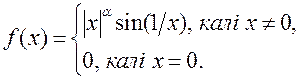 :
1) непарыўная; 2) мае вытворную; 3) мае
непарыўную вытворную?
:
1) непарыўная; 2) мае вытворную; 3) мае
непарыўную вытворную?
3.10.
Знайдзіце вытворныя
адваротных функцый і абсягі іх існавання для наступных функцый:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
3.11.
Знайдзіце вытворныя ![]() для функцый, якія зададзены параметрычна: 1)
для функцый, якія зададзены параметрычна: 1)
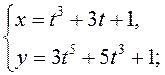 3)
3) 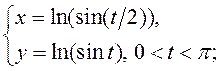 2)
2) 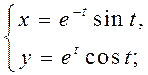 4)
4) 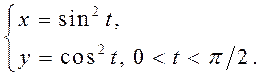
3.12.
Пакажыце, што функцыя ![]() , якая зададзена параметрычна, праўдзіцуь
адпаведную роўнасць:
1)
, якая зададзена параметрычна, праўдзіцуь
адпаведную роўнасць:
1) ![]() ,
,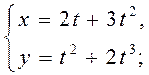 2)
2) ![]() ,
, 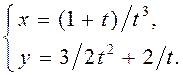
3.13.
Знайдзіце ![]() для функцый, зададзеных у палярных
каардынатах: 1)
для функцый, зададзеных у палярных
каардынатах: 1) ![]() (спіраль Архімеда) ; 2)
(спіраль Архімеда) ; 2) ![]() (кардыёіда) ;
3)
(кардыёіда) ;
3) ![]() (лагарыфмічная спіраль).
(лагарыфмічная спіраль).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.