3.14.
Знайдзіце ![]() у зададзеным пункце для наступных функцый:
1)
у зададзеным пункце для наступных функцый:
1) 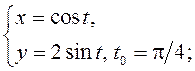 2)
2) 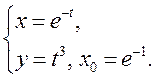
3.15.
Пакажыце, што функцыя 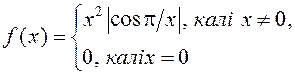 мае пункты недыферэнцавальнасці ў кожным
ваколлі пункта
мае пункты недыферэнцавальнасці ў кожным
ваколлі пункта ![]() =0, але з’яўляецца дыферэнцавальнай у гэтым
пункце.
=0, але з’яўляецца дыферэнцавальнай у гэтым
пункце.
3.16.
Ці будуць праўдзівымі
сцверджанні:
1).“Калі ![]() мае вытворную ў пункце,
мае вытворную ў пункце, ![]() , а
, а ![]() не мае вытворнай у пункце
не мае вытворнай у пункце![]() , то
а)
, то
а) ![]() не мае вытворнай у пункце
не мае вытворнай у пункце ![]() ; б)
; б) ![]() не мае вытворнай у пункце
не мае вытворнай у пункце ![]() ”.
2).“Калі
”.
2).“Калі ![]() і
і ![]() не маюць вытворных у пункце
не маюць вытворных у пункце ![]() , то
а)
, то
а) ![]() не мае вытворнай у пункце
не мае вытворнай у пункце ![]() ; б)
; б) ![]() не мае вытворнай у пункце
не мае вытворнай у пункце ![]() ”?
(Калі сцверджанне ёсць непраўдзівае, падайце адпаведны прыклад.)
”?
(Калі сцверджанне ёсць непраўдзівае, падайце адпаведны прыклад.)
3.17.
Ці будуць праўдзівымі
сцверджанні:
1) “Калі ![]()
![]() , то
, то ![]()
![]() ”.
2) “Калі
”.
2) “Калі ![]()
![]() , то
, то ![]()
![]() “.
3)“Калі
“.
3)“Калі ![]() і
і ![]()
![]() , то
, то ![]()
![]() ”?
”?
3.18.
Ці будуць праўдзівымі
наступныя сцверджанні:
1) “Для таго каб дыферэнцавальная на ![]() функцыя
функцыя ![]() мела мана-тонную на
мела мана-тонную на ![]() вытворную, неабходна, каб
вытворную, неабходна, каб ![]() была манатоннай на
была манатоннай на ![]() ”. “;
2) “Для таго каб дыферэнцавальная на
”. “;
2) “Для таго каб дыферэнцавальная на ![]() функцыя
функцыя ![]() мела мана-тонную на
мела мана-тонную на ![]() вытворную, дастаткова, каб
вытворную, дастаткова, каб ![]() была манатоннай на
была манатоннай на ![]() ”
3) “Для таго каб дыферэнцавальная функцыя мела перыядычную
вытворную, неабходна, каб функцыя была перыядычнай”.
4) “Для таго каб дыферэнцавальная функцыя мела перыядычную
вытворную, дастаткова, каб функцыя была перыядычнай”?
”
3) “Для таго каб дыферэнцавальная функцыя мела перыядычную
вытворную, неабходна, каб функцыя была перыядычнай”.
4) “Для таго каб дыферэнцавальная функцыя мела перыядычную
вытворную, дастаткова, каб функцыя была перыядычнай”?
3.19. Дакажыце, што вытворная цотнай функцыі ёсць функцыя няцотная, а няцотнай – цотная.
3.20.
Падайце прыклад
функцыі, якая мае вытворную ўсюды, за выклю-чэннем пунктаў ![]() ,
, ![]() ,
, ![]() .
.
3.21.
Падайце прыклад
складанай функцыі ![]() , якая мае вытворную ў пункце
, якая мае вытворную ў пункце ![]() і для якой:
1)
і для якой:
1) ![]() існуе,
існуе, ![]() не існуе; 2)
не існуе; 2) ![]() не існуе,
не існуе, ![]() існуе; 3)
існуе; 3) ![]() і
і ![]() не існуюць (тут
не існуюць (тут ![]() ).
).
1º. Геаметрычны сэнс
вытворных. Калі функцыя ![]() мае вытворную ў пункце
мае вытворную ў пункце ![]() , тады
, тады ![]() з’яўляецца вуглавым каэфіцыентам датычнай да
графіка функцыі
з’яўляецца вуглавым каэфіцыентам датычнай да
графіка функцыі ![]() у пункце
у пункце ![]() . У гэтым выпадку датычная і нармаль да крывой
. У гэтым выпадку датычная і нармаль да крывой
![]() у пункце
у пункце ![]() задаюцца адпаведна раўнаннямі:
задаюцца адпаведна раўнаннямі:
![]() – датычная,
– датычная, 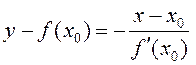 – нармаль.
– нармаль.
Калі ![]() непарыўная ў пункце
непарыўная ў пункце ![]() і
і ![]() , то графік функцыі ў гэтым пункце мае вертыкальную
датычную і гарызантальную нармаль, якія адпаведна задаюцца наступнымі
раўнаннямі:
, то графік функцыі ў гэтым пункце мае вертыкальную
датычную і гарызантальную нармаль, якія адпаведна задаюцца наступнымі
раўнаннямі: ![]() – датычная,
– датычная, ![]() – нармаль.
– нармаль.
Калі ![]() , то раўнанне нармалі мае выгляд
, то раўнанне нармалі мае выгляд ![]() .
.
2º. Фізічны сэнс
вытворных. Вытворная функцыі ![]() у пункце
у пункце ![]() ёсць імгненная хуткасць змянення гэтай
функцыі ў пункце
ёсць імгненная хуткасць змянення гэтай
функцыі ў пункце ![]() .
.
Прыклад 1. Запісаць раўнанні датычнай і нармалі да графіка
крывой ![]() ,
, ![]() у пунктах: а)
у пунктах: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
►Знойдзем вытворную паводле правіла вылічэння вытворнай функцыі,
зададзенай параметрычна: ![]() .
.
а) Калі ![]() , то
, то ![]() ,
, ![]() ,
, ![]() . Тады
. Тады ![]() – раўнанне датычнай,
– раўнанне датычнай, ![]() – раўнанне нармалі.
– раўнанне нармалі.
б) Калі ![]() , то
, то ![]() ,
, ![]() . Атрымліваем:
. Атрымліваем: ![]() – раўнанне датычнай,
– раўнанне датычнай, ![]() – раўнанне нармалі.
– раўнанне нармалі.
в)
Пры ![]() маем
маем ![]() і
і
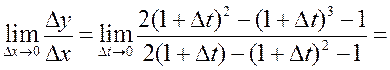
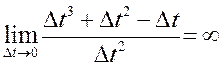 На падставе сказанага вышэй, датычная мае раўнанне
На падставе сказанага вышэй, датычная мае раўнанне ![]() , а нармаль –
, а нармаль – ![]() .◄
.◄
Прыклад 2. Пад якім вуглом перасякаюцца крывыя ![]() і
і ![]() ?
?
►Пад вуглом паміж дзвюма крывымі разумеюць вугал паміж
іх датычнымі ў пункце перасячэння крывых. Тангенс вугла паміж дзвюма прамымі ![]() і
і ![]() можна знайсці паводле формулы
можна знайсці паводле формулы 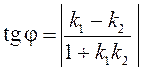 . Пункты перасячэння крывых знойдзем як
развязкі сіс-тэмы раўнанняў:
. Пункты перасячэння крывых знойдзем як
развязкі сіс-тэмы раўнанняў: 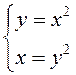 . Атрымліваем два пункты:
. Атрымліваем два пункты:![]() і
і ![]() . Цяпер вылічым вытворныя разгляданых функцый:
. Цяпер вылічым вытворныя разгляданых функцый:
![]()
![]() ,
, ![]() . Калі
. Калі ![]() і
і ![]() ёсць вуглавыя каэфіцыенты датычных да
графікаў функцый ў пункце
ёсць вуглавыя каэфіцыенты датычных да
графікаў функцый ў пункце ![]() , то
, то ![]() ,
, ![]() і
і 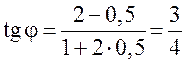 , а
, а ![]() . Разгледзім цяпер пункт
. Разгледзім цяпер пункт ![]() . Калі
. Калі ![]() , то
, то ![]() , і графік функцыі
, і графік функцыі ![]() датыкаецца да восі
датыкаецца да восі ![]() . Калі ж
. Калі ж ![]() , то
, то![]() , і графік гэтай функцыі датыкаецца да восі
, і графік гэтай функцыі датыкаецца да восі ![]() . Такім чынам, вугал паміж крывымі
. Такім чынам, вугал паміж крывымі ![]() і
і ![]() у пункце
у пункце ![]() будзе роўны
будзе роўны ![]() .◄
.◄
Прыклад 3. Колькасць цеплыні ![]() Дж, неабходнай для награвання 1 кг вады ад
Дж, неабходнай для награвання 1 кг вады ад ![]() да
да ![]() , вызначаецца формулай
, вызначаецца формулай ![]() . Знайсці цеплаёмістасць вады пры
. Знайсці цеплаёмістасць вады пры ![]() .
.
►Цеплаёмістасцю ![]() рэчыва называецца фізічная велічыня, лікава
роўная хуткасці змянення колькасці цеплыні. Таму
рэчыва называецца фізічная велічыня, лікава
роўная хуткасці змянення колькасці цеплыні. Таму ![]() . Калі ў апошнюю роўнасць падставіць значэнне
. Калі ў апошнюю роўнасць падставіць значэнне ![]() , то атрымаем
, то атрымаем ![]() . ◄
. ◄
3.22. Для зададзенай крывой у зададзеным пункце складзіце раўнанне а) датычнай;
б) нармалі:
1) ![]() ,
, ![]() ; 2)
; 2) ![]() ,
, ![]() ; 3)
; 3) ![]() ,
, ![]() ; 4)
; 4) ![]() ,
, ![]() ; 5)
; 5) ![]() ,
, ![]() ,
, ![]() ; 6)
; 6) ![]() ,
, ![]() ,
, ![]() ; 7)
; 7) ![]() ,
, ![]() ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.