3.130. Дакажыце наступныя сцверджанні:
1. Калі ![]() і
і ![]() - два суседнія стацыянарныя пункты дыферэнцавальнай
функцыі
- два суседнія стацыянарныя пункты дыферэнцавальнай
функцыі ![]() (між імі
няма іншых стацыянарных пунктаў), то на адрэзку
(між імі
няма іншых стацыянарных пунктаў), то на адрэзку ![]() функцыя
функцыя ![]() манатонная.
2. Не існуе дыферэнцавальнай функцыі, якая мае ў абодвух суседніх стацыянарных
пунктах лакальныя максімумы або лакальныя міні-мумы.
3. Дыферэнцавальная функцыя, якая мае ў кожным стацыянарным пункце перегін,
з’яўляецца манатоннай.
4. Паміж двума пунктамі экстрэмуму дыферэнцавальнай функцыі існуе прынамсі
адзін пункт перагіну.
5. Калі мнагасклад цотнай ступені мае толькі адзін стацыянарны пункт, то ён
з’яўляецца пунктам экстрэмуму.
6. Калі мнагасклад няцотнай ступені мае толькі адзін стацыянарны пункт, то ў
гэтым пункце – перагін.
7. Калі мнагасклад цотнай ступені мае толькі два стацыянарныя пункты, то адзін
з іх ёсць пункт эксрэмуму, а другі – пункт перагіну.
8. Калі мнагасклад няцотнай ступені мае толькі два стацыянарныя пункты, то
кожны з іх з’яўляецца або пунктам экстрэмуму, або пунктам перагіну.
9. Калі функцыя
манатонная.
2. Не існуе дыферэнцавальнай функцыі, якая мае ў абодвух суседніх стацыянарных
пунктах лакальныя максімумы або лакальныя міні-мумы.
3. Дыферэнцавальная функцыя, якая мае ў кожным стацыянарным пункце перегін,
з’яўляецца манатоннай.
4. Паміж двума пунктамі экстрэмуму дыферэнцавальнай функцыі існуе прынамсі
адзін пункт перагіну.
5. Калі мнагасклад цотнай ступені мае толькі адзін стацыянарны пункт, то ён
з’яўляецца пунктам экстрэмуму.
6. Калі мнагасклад няцотнай ступені мае толькі адзін стацыянарны пункт, то ў
гэтым пункце – перагін.
7. Калі мнагасклад цотнай ступені мае толькі два стацыянарныя пункты, то адзін
з іх ёсць пункт эксрэмуму, а другі – пункт перагіну.
8. Калі мнагасклад няцотнай ступені мае толькі два стацыянарныя пункты, то
кожны з іх з’яўляецца або пунктам экстрэмуму, або пунктам перагіну.
9. Калі функцыя ![]() мае
мае
![]() вытворную ў
ваколлі пункта
вытворную ў
ваколлі пункта ![]() і
і ![]() то пры
цотным
то пры
цотным ![]() пункт
пункт ![]() з’яўляецца
пунктам перагіу, а пры няцотным – пунктам экстрэмуму.
з’яўляецца
пунктам перагіу, а пры няцотным – пунктам экстрэмуму.
3.131.
Знайдзіце раўнанні
асімптот да графікаў функцый:
1)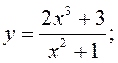 2)
2)![]() 3)
3)![]() 4)
4)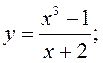 5)
5)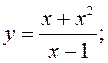 6)
6)![]() 7)
7)![]()
3.132.
Даследуйце функцыі і
пабудуйце іх графікі:
1) ![]() 2)
2) ![]() 3)
3) ![]()
3.133. Паводле формулы Радрыга паліномы Лежандра
азначаюцца наступным чынам: ![]() Пабудуйце
графікі паліномаў Лежандра: 1)
Пабудуйце
графікі паліномаў Лежандра: 1) ![]() ;
2)
;
2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
3.134.
Даследуйце функцыі і
пабудуйце іх графікі:
1) 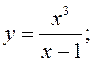 2)
2) 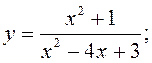 3)
3) ![]() 4)
4) ![]() 5)
5) 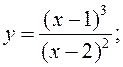 6)
6) ![]() 7)
7) 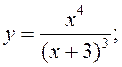 8)
8) 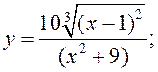 9)
9) ![]() ; 10)
; 10) ![]() 11)
11) ![]() ; 12)
; 12) 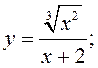 13)
13) ![]() 14)
14) ![]() 15)
15) ![]() 16)
16) ![]() 17)
17) ![]() 18)
18) ![]() 19)
19) ![]() ; 20)
; 20) ![]() 21)
21) ![]() 22)
22) ![]() 23)
23)![]()
3.135.
Пабудуйце графікі
функцый, зададзеных у параметрычнай форме:
1) ![]() 2)
2)
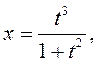
 3)
3) ![]() 4)
4) ![]() 5)
5) ![]() 6)
6) ![]()
3.136. Дадатны лік a раскладзіце на множнікі так, каб іх сума была найбольшай.
3.137. У круг радыуса R умежце прамавугольнік найбольшай плошчы.
3.138. У круг радыуса R умежце трохвугольнік найбольшай плошчы.
3.139. У шар радыуса R умежце правільную чатырохвугольную прызму найбольшага аб’ёму.
3.140. У шар радыуса R умежце цыліндр найбольшага аб’ёму.
3.141. Які з конусаў, акрэсленых вакол шара, мае найменшы аб’ём?
3.142. Знайдзіце пункт на парабале ![]() , адлегласць
ад якога да пункта (3; 1) найменшая.
, адлегласць
ад якога да пункта (3; 1) найменшая.
3.143. Знайдзіце найменшую даўжыню адрэзка, што дзеліць роўнастаронні трохвугольнік са стараной а на дзве роўнавялікія фігуры.
3.144. Да парабалы ![]() правядзіце
нармаль, якая адсякае ад яе сегмент найменшай плошчы.
правядзіце
нармаль, якая адсякае ад яе сегмент найменшай плошчы.
3.145. З якога пункта восі ![]() адрэзак на
восі
адрэзак на
восі ![]() , што ляжыць
паміж пунктамі (0; 1) і (0; 4) відаць пад найбольшым вуглом?
, што ляжыць
паміж пунктамі (0; 1) і (0; 4) відаць пад найбольшым вуглом?
3.146. Знайдзіце найбольшы аб’ём
конуса з дадзенай утваральнай ![]()
3.147. Цыліндр накрыты зверху паўшарам такога ж радыуса. Пры якім радыусе поўная паверхня цела будзе найменшай, калі аб’ём цела роўны V?
3.148. У конус радыуса R і вышыні H умежаны цыліндр найбольшага аб’ёму. Знайдзіце радыус r і вышыню h гэтага цыліндра.
3.149. З круглага ліста бляхі выразаны сектар і скручаны ў выглядзе канічнай варонкі. Якім павінен быць вугал сектара, каб варонка мела найменшы аб’ём?
3.150. З круглага бруса дыяметрам d выпілоўваецца бэлька прамавугольнага сячэння, аснова якой роўная b, а вышыня h. Пры якіх памерах бэлька будзе найбольш трывалай, калі яе трываласць прапарцыянальная bh.
3.151. З металу неабходна выліць, а потым адшліфаваць трохвугольную прызму з роўнастаронняй асновай. Шліфоўка адзінкі плошчы трохвугольнай грані каштуе m рублёў, а прамавугольнай – n рублёў. Пры дадзеным аб’ёме V вызначце памеры прызмы так, каб кошт шліфоўкі быў найменшым.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.