3.107.
Вылічыце з дапамогай
формулы Тэйлара з дадзенай дакладнасцю:
1) ![]() да
да ![]() ; 2)
; 2)
![]() да
да ![]() ; 3)
; 3)
![]() да
да ![]() ;
;
4) ![]() да
да ![]() ; 5)
; 5)
![]() да
да ![]() ; 6)
; 6)
![]() да
да ![]() ;
;
7) ![]() да
да ![]() ; 8)
; 8)
![]() да
да ![]() ; 9)
; 9)
![]() да
да ![]() .
.
3.108.
Дакажыце
ірацыянальнасць лікаў ![]() ,
, ![]() ,
, ![]() .
.
3.109.
Знайдзіце такія лікі ![]() і
і ![]() , каб:
1)
, каб:
1) 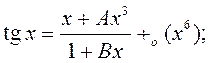 2)
2) ![]() .
.
3.110.
Няхай ![]() - двойчы дыферэнцавальная функцыя на
- двойчы дыферэнцавальная функцыя на ![]() і няхай
і няхай ![]() верхнія межы
функцый
верхнія межы
функцый ![]() ,
, ![]() ,
, ![]() . Дакажыце,
што
. Дакажыце,
што ![]() .
.
3.111.
Няхай ![]() - двойчы дыферэнцавальная функцыя на
- двойчы дыферэнцавальная функцыя на ![]() ,
, ![]() абмежаваная
на
абмежаваная
на ![]() і
і ![]() , калі
, калі ![]() . Дакажыце,
што
. Дакажыце,
што ![]() , калі
, калі ![]() .
.
3.112.
Вылічыце кратнасць
нуля функцыі ў дадзеным пункце ![]() :
1)
:
1) ![]() ,
,![]() ; 2)
; 2)
![]() ,
, ![]() ; 3)
; 3)
![]()
![]() ;
4)
;
4) ![]() ,
, ![]() ; 5)
; 5) ![]() ,
, ![]() ; 6)
; 6) ![]() ,
, ![]() ;
7)
;
7) ![]() ,
, ![]() ; 8)
; 8) ![]() ,
, ![]() .
.
3.113. Дастасуйце формулу Тэйлара для доказу правіла Лёпіталя.
3.114. З формулы Тэйлара атрымайце формулу бінома Ньютана.
3.115.
Дакажыце наступныя
сцверджанні:
1) Калі функцыя ![]() мае
ў пункце
мае
ў пункце ![]() вытворную
другога парадку, то
вытворную
другога парадку, то
![]() ,
,
![]()
2)
Ці магчымая такая функцыя ![]() ,
што існуе
,
што існуе ![]() , але яна не
мае вытворнай другога парадку.
, але яна не
мае вытворнай другога парадку.
3.116.
Дастасуйце формулы
Маклёрэна вядомых функцый для вылічэння лімітаў:
1) ![]() 2)
2) 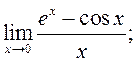 3)
3) 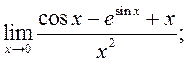 4)
4) 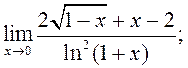 5)
5) 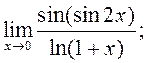 6)
6) ![]() 7)
7) ![]() 8)
8) 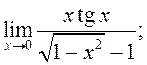 9)
9) 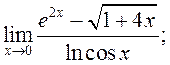 10)
10) 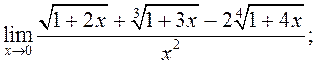 11)
11) 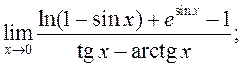 12)
12) 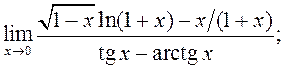 13)
13) 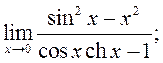 14)
14) 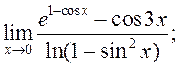 15)
15) 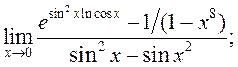 16)
16)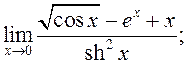 17)
17) 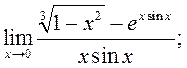 18)
18) 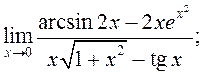 19)
19)
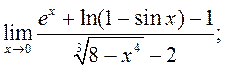 20)
20) ![]() 21)
21) ![]() 22)
22) ![]() 23)
23) ![]() 24)
24) ![]() 25)
25) ![]() 26)
26) ![]() 27)
27) ![]()
![]() 28)
28) ![]() 29)
29) ![]() 30)
30) 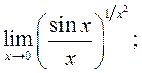 31)
31) 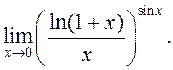
Функцыя ![]() называется
нарастальнай (спадальнай) на інтэрвале
называется
нарастальнай (спадальнай) на інтэрвале ![]() , калі для
адвольных
, калі для
адвольных ![]() ,
, ![]() ,
, ![]() мае месца
няроўнасць
мае месца
няроўнасць ![]()
![]() . Дыферэнцавальная
функцыя
. Дыферэнцавальная
функцыя ![]() з’яўляецца
нарастальнай (спадальнай), калі
з’яўляецца
нарастальнай (спадальнай), калі ![]()
![]() . Калі словы
“нарастальная (спадальная)” замяніць на “строга нарастальная (спадальная)”,
то ўсе знакі ў азначаных няроўнасцях трэба замяніць на строгія.
. Калі словы
“нарастальная (спадальная)” замяніць на “строга нарастальная (спадальная)”,
то ўсе знакі ў азначаных няроўнасцях трэба замяніць на строгія.
Пункт ![]() называецца
пунктам лакальнага экстрэмуму функцыі
называецца
пунктам лакальнага экстрэмуму функцыі ![]() , калі існуе
такое яго ваколле, што для ўсіх пунктаў ваколля мае месца адна з няроўнасцяў:
1)
, калі існуе
такое яго ваколле, што для ўсіх пунктаў ваколля мае месца адна з няроўнасцяў:
1) ![]() , 2)
, 2) ![]() . У выпадку 1)
пункт
. У выпадку 1)
пункт ![]() называецца
пунктам максімуму, у выпадку 2) – пунктам мінімуму
функцыі
называецца
пунктам максімуму, у выпадку 2) – пунктам мінімуму
функцыі ![]() . Калі
. Калі ![]() , то пункт
, то пункт ![]() называецца стацыянарным.
Стацыянарныя пункты і ізаляваныя пункты, у якіх вытворная не існуе, называюцца крытычнымі.
называецца стацыянарным.
Стацыянарныя пункты і ізаляваныя пункты, у якіх вытворная не існуе, называюцца крытычнымі.
Няхай функцыя ![]() дыферэнцавальная
ў некаторым працятым ваколлі пункта
дыферэнцавальная
ў некаторым працятым ваколлі пункта ![]() і
непарыўная ў пункце
і
непарыўная ў пункце ![]() .
Калі пры
.
Калі пры ![]() вытворная
вытворная ![]()
![]() , а пры
, а пры ![]() вытворная
вытворная ![]()
![]() , то
, то ![]() – пункт
максімуму (мінімуму). Двойчы дыферэнцавальная функцыя
– пункт
максімуму (мінімуму). Двойчы дыферэнцавальная функцыя ![]() мае максімум
(мінімум) у пункце
мае максімум
(мінімум) у пункце ![]() ,
калі
,
калі ![]()
![]() .
.
Функцыя ![]() называецца
выпуклай уніз (уверх) на інтэрвале
называецца
выпуклай уніз (уверх) на інтэрвале ![]() , калі для
адвольных пунктаў
, калі для
адвольных пунктаў ![]() і
і ![]() з гэтага
прамежку і адвольных лікаў
з гэтага
прамежку і адвольных лікаў ![]() такіх,
што
такіх,
што ![]() ,
, ![]() ,
, ![]() , мае месца
няроўнасць
, мае месца
няроўнасць ![]()
![]() . Двойчы ды-ферэнцавальная
функцыя
. Двойчы ды-ферэнцавальная
функцыя ![]() ёсць выпуклая
ўніз (ўверх) на
ёсць выпуклая
ўніз (ўверх) на ![]() ,
калі
,
калі ![]()
![]() для
для ![]() . Пункт, у
якім функцыя мяняе кірунак выпукласці, называецца пунктам перагіну.
Калі пункт
. Пункт, у
якім функцыя мяняе кірунак выпукласці, называецца пунктам перагіну.
Калі пункт ![]() з’яўляецца
пунктам перагіну, то або
з’яўляецца
пунктам перагіну, то або ![]() ,
або
,
або ![]() не існуе.
не існуе.
Экстрэмумы функцыі знаходзяць паводле наступнага правіла:
1. Знаходзяць вытворную ![]() .
.
2. Прыраўноўваюць яе да нуля і знаходзяць стацыянарныя пункты функцыі; вызначаюць пункты, у якіх вытворная не існуе.
3. Даследуюць знакі вытворнай у ваколлі крытычных пунктаў. Калі пры пераходзе праз крытычны пункт вытворная мяняе знак з дадатнага на адмоўны, то ў гэтым пункце функцыя мае лакальны максімум, калі, наадварот, з адмоўнага на дадатны, – мінімум.
Для вызначэння экстрэмуму двойчы дыферэнцавальнай функцыі высвятляюць
знак вытворнай другога парадку ў стацыянарным пункце ![]() . Калі
. Калі ![]() , то функцыя ў
гэтым пункце дасягае максімуму, калі
, то функцыя ў
гэтым пункце дасягае максімуму, калі ![]() ,
то функцыя мае мінімум.
,
то функцыя мае мінімум.
Прыклад 1. Знайдзіце экстрэмумы функцыі ![]()
►Да разгляданай функцыі дастасуем пададзенае вышэй правіла.
1. 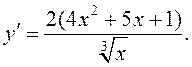 2. Функцыя
мае стацыянарныя пункты
2. Функцыя
мае стацыянарныя пункты ![]() ,
,
![]() . У пункце
. У пункце ![]() вытворная не
існуе. 3. На прамежках
вытворная не
існуе. 3. На прамежках ![]() ,
,
![]() вытворная
адмоўная, а на прамежках
вытворная
адмоўная, а на прамежках ![]() ,
,
![]() - дадатная.
Пры пераходзе праз пункты
- дадатная.
Пры пераходзе праз пункты ![]() і
і
![]() вытворная
мяняе знак з мінуса на плюс, і значыць, гэтыя пункты з’яўляюцца пунктамі
мінімуму, а пры пераходзе праз пункт
вытворная
мяняе знак з мінуса на плюс, і значыць, гэтыя пункты з’яўляюцца пунктамі
мінімуму, а пры пераходзе праз пункт ![]() вытворная
мяняе знак з плюса на мінус, і ў гэтым пункце функцыя дасягае лакальнага
максімуму. ◄
вытворная
мяняе знак з плюса на мінус, і ў гэтым пункце функцыя дасягае лакальнага
максімуму. ◄
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.