![]() .
(3.18)
.
(3.18)
►Знойдзем першы дыферэнцыял ад абедзвюх частак роўнасці (3.18):
![]() ,
(3.19)
,
(3.19)
а затым дыферэнцыял ад (3.19):
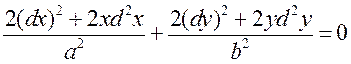 . (3.20)
. (3.20)
Зменная
![]() незалежная,
таму
незалежная,
таму ![]() . Тады з
(3.20) маем
. Тады з
(3.20) маем
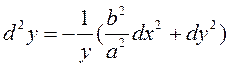 (3.21)
(3.21)
З
(3.19) знойдзем 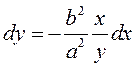 і
падставім у (3.21). Канчаткова маем
і
падставім у (3.21). Канчаткова маем
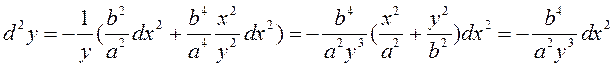 . ◄
. ◄
3.73. Знайдзіце вытворную другога парадку ад наступных функцый:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ;
7)
;
7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ; 11)
; 11) ![]() ; 13)
; 13) ![]() ; 14)
; 14) ![]() 10)
10) ![]() ; 12)
; 12) ![]() ; .
; .
3.74.
Пункт рухаецца
прамалінейна паводле закону ![]() . Знайдзіце паскарэнне праз 2 с ад пачатку
руху.
. Знайдзіце паскарэнне праз 2 с ад пачатку
руху.
3.75.
Знайдзіце велічыню
сілы, што дзейнічае на пункт з масай ![]() , у момант часу
, у момант часу ![]() =1, калі пункт рухаецца паводле закону
=1, калі пункт рухаецца паводле закону ![]() .
.
3.76.
Пакажыце, што
наступныя функцыі праўдзяць дадзеныя раўнанні:
1) ![]() ,
, ![]() ;
2)
;
2) ![]() ,
, ![]() ;
3)
;
3) ![]() ,
, ![]() ;
4)
;
4) ![]() ,
, ![]() ;
5)
;
5) ![]() ,
, ![]() ;
6)
;
6) ![]() ,
, ![]() .
.
3.77.
Вылічыце дыферэнцыялы
другога парадку ў дадзеным пункце ![]() для наступных функцый, калі
для наступных функцый, калі ![]() - незалежная зменная:
1)
- незалежная зменная:
1) ![]() ,
, ![]() = 1; 2)
= 1; 2) ![]() ,
, ![]() = 0;
3)
= 0;
3) ![]() ,
, ![]() ; 4)
; 4) ![]() ,
, ![]() = 1;
= 1;
5) ![]() ,
, ![]() =6; 6)
=6; 6) ![]() ,
, ![]() .
.
3.78.
Знайдзіце ![]() для функцый, зададзеных параметрычна:
1)
для функцый, зададзеных параметрычна:
1) ![]() ,
, ![]() ; 2)
; 2) ![]() ,
, ![]() ;
3)
;
3) ![]() ,
, ![]() ; 4)
; 4) ![]() ,
, ![]() ;
5)
;
5) ![]() ,
, ![]() ; 6)
; 6) ![]() ,
, ![]() ;
7)
;
7) ![]() ,
, ![]() ;
; ![]() .
.
3.79.
Знайдзіце ![]() і
і ![]() , калі
, калі ![]() і
і ![]() – вядомыя функцыі ад
– вядомыя функцыі ад ![]() :
1)
:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() .
.
3.80.
Знайдзіце ![]() для функцый, зададзеных няяўна:
1)
для функцый, зададзеных няяўна:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() .
.
3.81.
Знайдзіце ![]() для наступных функцый:
1)
для наступных функцый:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ;
5)
;
5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)..
; 8)..![]() .
.
3.82.
Знайдзіце вытворную зададзенага
парадку ![]() ў пункце
ў пункце ![]() для наступных функцый:
1)
для наступных функцый:
1) ![]() ,
, ![]() = 10 ,
= 10 , ![]() = 2 ; 2)
= 2 ; 2) ![]() ,
, ![]() = 50 ,
= 50 , ![]() = 0 ;
3)
= 0 ;
3) ![]() ,
, ![]() = 3 ,
= 3 , ![]() = 1 ; 4)
= 1 ; 4) ![]() ,
, ![]() = 100 ,
= 100 , ![]() = 0 ; 5)
= 0 ; 5) ![]() ,
, ![]() = 20 ,
= 20 , ![]() = 1 ; 6)
= 1 ; 6) ![]() ,
, ![]() = 6,
= 6, ![]() = 0.
= 0.
3.83.
Знайдзіце ![]() зададзенага парадку
зададзенага парадку ![]() калі
калі ![]() ёсць незалежная змен-ная:
1)
ёсць незалежная змен-ная:
1) ![]() ,
, ![]() ; 2)
; 2) ![]() ,
, ![]() ; 3)
; 3) ![]() ,
, ![]() ; 4)
; 4) ![]() ,
, ![]() ; 5)
; 5) ![]() ,
, ![]() .
.
3.84.
Знайдзіце ![]() (
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – зададзены):
1)
– зададзены):
1) ![]() ; 2)
; 2) ![]() .
.
3.85.
Знайдзіце ![]() функцыі
функцыі ![]() , зададзенай няяўна:
1)
, зададзенай няяўна:
1) ![]() ; 2)
; 2) ![]() .
.
3.86.
Вызначце, якога
парадку вытворныя існуюць у дадзеных функцый у пункце ![]() =0:
1)
=0:
1) ![]() ; 2)
; 2) 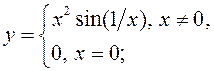 3)
3) 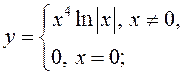 4)
4) 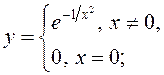 5)
5) 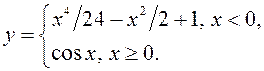
3.87.
Атрымайце формулу для
другой вытворнай функцыі ![]() .
.
3.88.
Калі функцыя мае
першую вытворную ![]() , то яна мае і вытворныя ўсіх парадкаў.
Дакажыце гэта.
, то яна мае і вытворныя ўсіх парадкаў.
Дакажыце гэта.
3.89.
Калі функцыя мае ![]() -ю вытворную і
-ю вытворную і ![]() , то яна мае і вытворныя ўсіх парадкаў.
Дакажыце гэта.
, то яна мае і вытворныя ўсіх парадкаў.
Дакажыце гэта.
3.90.
Функцыя ![]() двойчы дыферэнцавальная і
двойчы дыферэнцавальная і
![]() , дзе
, дзе ![]() і
і ![]() маюць вытворныя ўсіх парадкаў. Дакажыце, што
функцыя
маюць вытворныя ўсіх парадкаў. Дакажыце, што
функцыя
![]() мае вытворныя ўсіх парадкаў.
мае вытворныя ўсіх парадкаў.
3.91.
Функцыя ![]()
![]() раз дыферэнцавальная і
раз дыферэнцавальная і 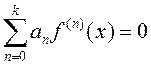 ,
, ![]() . Дакажыце , што функцыя
. Дакажыце , што функцыя ![]() мае вытворныя ўсіх парадкаў.
мае вытворныя ўсіх парадкаў.
Няхай функцыі ![]() і
і ![]() дыферэнцавальныя
ў ваколлі пункта
дыферэнцавальныя
ў ваколлі пункта ![]() , за
выключэннем, можа быць, пункта
, за
выключэннем, можа быць, пункта ![]() ,
прычым 1)
,
прычым 1) ![]() , 2)
, 2) ![]()
![]() ,
, ![]()
![]() пры
пры ![]() , 3) існуе
, 3) існуе 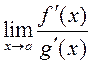 . Тады існуе
. Тады існуе
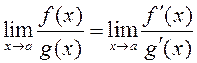 .
.
Прыклад 1. Знайсці 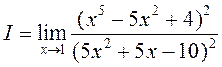 .
.
►У дадзеным выпадку маем нявызначанасць тыпу ![]() . Для функцый
. Для функцый ![]() і
і ![]() выкананы ўсе
ўмовы правіла Лапіталя ў ваколлі пункта
выкананы ўсе
ўмовы правіла Лапіталя ў ваколлі пункта ![]() . Таму
. Таму 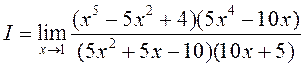 , і зноў
атрымліваем нявызначанасць тыпу
, і зноў
атрымліваем нявызначанасць тыпу ![]() .
Для функцый, якія знаходзяцца ў назоўніку і лічніку апошняга выразу, таксама
выкананы
.
Для функцый, якія знаходзяцца ў назоўніку і лічніку апошняга выразу, таксама
выкананы
ўсе ўмовы правіла Лёпіталя. Дастасуем яго яшчэ раз і атрымаем 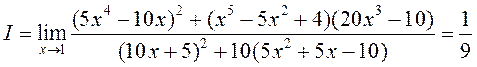 . ◄
. ◄
Каб дастасаваць правіла Лёпіталя да нявызначанасцяў
тыпу ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() неабходна іх
пераўтварыць да нявызначанасці тыпу
неабходна іх
пераўтварыць да нявызначанасці тыпу ![]() або
або
![]() .
.
Прыклад 2. Знайсці ![]() .
.
►Маем нявызначанасць тыпу ![]() .
З формулы
.
З формулы ![]() і
непарыўнасці функціі
і
непарыўнасці функціі ![]() пры
ўсіх w атрымаем
пры
ўсіх w атрымаем ![]() . Дастасуем
правіла Лёпіталя да атрыманага ліміту, які знаходзіцца ў паказніку
. Дастасуем
правіла Лёпіталя да атрыманага ліміту, які знаходзіцца ў паказніку 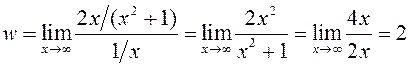 . Адкуль
. Адкуль ![]() . ◄
. ◄
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.