Дыферэнцыяльнае злiчэнне функцый адной зменнай. Вытворная. Формулы i правiлы вылiчэння вытворных, страница 3

3.23.  Запішыце раўнанні датычнай і нармалі да крывой  у пунктах: 1)  ;  2) ;  3) .

3.24.  Дакажыце, што пры ўсякім становішчы ўтваральнай акружыны цыклоіды датычная да яе ў адпаведным пункце праходзіць праз найвышэйшы пункт акружыны, а нармаль – праз найніжэйшы.

3.25.  Знайдзіце пункты, у якіх датычная да графіка функцыі параллельная восі , калі функцыя зададзена наступным чынам: 1) ;                       2) ; 3) , ;  4) , .

3.26.  Вызначце, які вугал утварае з воссю  датычная да крывой  у пункце .

3.27.  Запішыце раўнанне той нармалі да крывой , якая параллельная прамой .

3.28.  Пакажыце, што ў двух пунктах кардыёіды  , , якія адпавядаюць такім значэнням параметра  і , што розніца паміж імі роўная  , датычныя параллельныя.

3.29.  Дакажыце, што крывая : а) датыкаецца да восі  , калі ; б) датыкаецца да восі , калі .

3.30.  Дакажыце, што ў астроіды , , даўжыня адрэзку датычнай, які знаходзіцца паміж восямі кардынат, ёсць велічыня сталая.

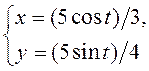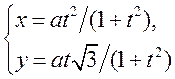3.31.  Вызначце, у якім пункце і пад якім вуглом перасякаюцца крывыя: 1)  і ;                        2)  і ; 3)  і ;                             4)  і ; 5)  і ; 6)  і ; 7)  і ;                 8)  і .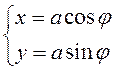

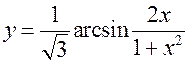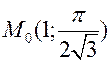3.32.  Вызначыце вугал паміж левай і правай датычнымі графіка функцыі  у пункце : 1) , ;    2) , ;    3) , ; 4) , ;  5)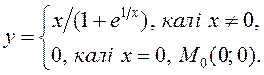 

3.33.  Пакажыце, што сем’і наступных крывых утвараюць артаганальную сетку, г. зн. крывыя гэтых сем’яў перасякаюцца пад прамымі вугламі:       1)  і  – гіпербалы; 2)   і   – парабалы; 3) , ,  – эліпсы і     , ,  – гіпербалы.

3.34.  Дакажыце, што крывая  датыкаецца да кожнай з ліній ,   ва ўсіх агульных з імі пунктах.

3.35.  Дакажыце, што калі  ёсць раўнанне крывой у палярнай сістыме кардынат, і  - вугал паміж датычнай і палярным радыусам пункта дотыку, то .

3.36.  Знайдзіце вугал паміж датычнай і палярным радыусам у пункце дотыку для наступных крывых:       1) гіпербалічнай  спіралі  ;  2) лагарыфмічнай  спіралі  ; 3) кардыёіды ; 4) дугі лемніскаты Бэрнулі , .

3.37.  Дакажыце, што вугал паміж датычнай да спіралі Архімеда  і палярным радыусам пункта дотыку імкнецца да , калі .

3.38.  Пад якім вуглом перасякаюцца крывыя  і  у пункце ?

3.39.  Запішыце ў дэкартавых і ў палярных кардынатах раўнанне нармалі да кардыёіды  у пункце з палярным вуглом .

3.40.  Радыус шара мяняецца з хуткасцю . З якой хуткасцю мяняюцца аб’ём і плошча паверхні шара?

3.41.  Пункт рухаецца па лагарыфмічнай спіралі . Знайдзіце хут-касць змянення палярнага радыуса, калі ён аварочваецца з вуглавой хуткасцю .

3.42.  Пункт рухаецца па акружыне . Знайдзіце хуткасць змянення абцысы і ардынаты пункта, калі палярны радыус аварочваецца з вуглавой хуткасцю . Палярная вось супадае з воссю абцысаў, полюс супадае з пачаткам дэкартавай сістэмы каардынат.

3.43.  Пры якім значэнні вугла сінус мяняецца ўдвая больш марудна за аргумент?

3.44.  Пры якім значэнні вугла хуткасці змянення сінуса і тангенса будуць аднолькавымі?

3.45.  Адлегласць, якая пройдзена матэрыяльным пунктам за час , ёсць  ( – у метрах).Знайдзіце хуткасць руху дадзенага пункта ў момант часу

3.46.  Дадзена раўнанне руху пункта па восі :   (– у метрах,  – у секундах). Знайдзіце хуткасць руху  і паскарэнне  гэтага пункта ў момант часу .

3.47.  Цела масай 3 кг рухаецца прамалінейна па закону  ( – у метрах,  – у секундах). Вылічыце кінетычную энергію  цела праз 5 с пасля пачатку руху.

3.48.  Напружанне на кандэнсатары мяняецца па сінусоіднаму закону  . Чаму роўная сіла зараднага току , які праходзіць праз кандэнсатар, калі , ?

3.49.  Залежнасць шляху ад часу пры прамалінейным руху пункта задаецца раўнаннем  ( – у секундах,   – у метрах). Вызначыце хуткасць руху ў канцы другой секунды.