ўзяць ![]() . Тады
. Тады
![]() ,
, ![]() .
.
Падставіўшы ўсё гэта ў формулу (3.8), знаходзім
![]() .◄
.◄
3.59.
Для функцыі ![]() знайдзіце
знайдзіце ![]() ,
, ![]() і параўнайце іх, калі: 1)
і параўнайце іх, калі: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
3.60. Раўнанне руху задаецца формулай ![]() , дзе
, дзе ![]() зададзена ў секундах, а
зададзена ў секундах, а ![]() – у метрах. Для моманту часу
– у метрах. Для моманту часу ![]() = 2 с. Знайдзіце
= 2 с. Знайдзіце ![]() – прырост шляху і
– прырост шляху і ![]() – дыферэнцыял шляху і параўнайце іх, калі: 1)
– дыферэнцыял шляху і параўнайце іх, калі: 1) ![]() с; 2)
с; 2) ![]() с; 3)
с; 3) ![]() с.
с.
3.61.
Пакажыце, што пры ![]() = 1 прырост функцыі
= 1 прырост функцыі ![]() нельга падаць у выглядзе (3.5) ні пры якім А,
таму
нельга падаць у выглядзе (3.5) ні пры якім А,
таму ![]() пры
пры ![]() не з’яўляецца дыферэнцавальнай. Вытлумачце
гэты вынік геаметрычна.
не з’яўляецца дыферэнцавальнай. Вытлумачце
гэты вынік геаметрычна.
3.62.
Няхай зададзена
дыферэнцавальная ў пункце ![]() функцыя
функцыя ![]() , і няхай у пункце
, і няхай у пункце ![]() зададзены прырост
зададзены прырост ![]() . Знайдзіце
. Знайдзіце ![]() у пункце
у пункце ![]() , калі галоўная лінейная частка прыросту
функцыі ў пункце
, калі галоўная лінейная частка прыросту
функцыі ў пункце ![]() , што адпавядае прыросту аргумента
, што адпавядае прыросту аргумента ![]() , стала роўнай 0,8.
, стала роўнай 0,8.
3.63.
Няхай ![]() , дзе
, дзе ![]() . Якія з наступных роўнасцяў будуць
правільнымі:
1)
. Якія з наступных роўнасцяў будуць
правільнымі:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ?
?
3.64.
Знайдзіце дыферэнцыял
функцыі ![]() :
1)
:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
3.65.
Знайдзіце дыферэнцыял
функцыі ![]() у зададзеным пункце:
1)
у зададзеным пункце:
1) ![]() ,
, ![]() ;
2)
;
2) ![]() ,
, ![]() ;
3)
;
3) ![]() ,
, ![]() ;
4)
;
4) ![]() ,
, ![]() ;
5)
;
5) ![]() ,
, ![]() ; 6)
; 6) ![]() ,
, ![]() ,
, ![]() ; 7)
; 7) ![]() ,
, ![]() ,
, ![]() ; 8)
; 8) ![]() ,
, ![]() ,
, ![]() .
.
3.66.
Пакажыце, што функцыя ![]() праўдзіць роў-насць
праўдзіць роў-насць ![]() .
.
3.67.
Пакажыце, што функцыя ![]() , якая задаецца няяўна раўнаннем
, якая задаецца няяўна раўнаннем ![]() , праўдзіць роўнасць
, праўдзіць роўнасць ![]() .
.
3.68.
Няхай ![]() ёсць дыферэнцавальныя функцыі ад
ёсць дыферэнцавальныя функцыі ад ![]() . Знайдзіце дыферэнцыял функцыі
. Знайдзіце дыферэнцыял функцыі ![]() (
(![]() лічацца вядомымі), калі:
1)
лічацца вядомымі), калі:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() .
.
3.69.
Дакажыце набліжаную
формулу ![]() , калі
, калі ![]() значна менш за
значна менш за ![]() . З дапамогай гэтай формулы вылічыце
набліжана:
1)
. З дапамогай гэтай формулы вылічыце
набліжана:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
3.70.
Вылічыце набліжанае
значэнне:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() , калі
, калі ![]() = 0,15.
= 0,15.
3.71.
Перыяд вагання ківача
(у секундах) вызначаецца паводле формулы ![]() , дзе
, дзе ![]() – даўжыня ківача (у сантыметрах) і
– даўжыня ківача (у сантыметрах) і ![]()
![]() . Маецца ківач з даўжынёй
. Маецца ківач з даўжынёй ![]() =20 см. На колькі трэба змяніць яго даўжыню,
каб перыяд
=20 см. На колькі трэба змяніць яго даўжыню,
каб перыяд ![]() павялічыўся на 0,05 с?
павялічыўся на 0,05 с?
3.72.
Для вызначэння
паскарэння сілы цяжару з дапамогай вагання ківа-ча выкарыстоўваюць формулу ![]() , дзе
, дзе ![]() – даўжыня ківача,
– даўжыня ківача, ![]() – поўны перыяд ваганняў. Як адаб’ецца на
значэнні
– поўны перыяд ваганняў. Як адаб’ецца на
значэнні ![]() рэлятыўная хібнасць
рэлятыўная хібнасць ![]() пры вылічэнні: а) даўжыні
пры вылічэнні: а) даўжыні ![]() ; б) перыяду
; б) перыяду ![]() ?
?
Калі існуе вытворная функцыі ![]() , то яе
называюць вытворнай другога парадку функцыі
, то яе
называюць вытворнай другога парадку функцыі ![]() і абазначаюць
і абазначаюць ![]() . Аналагічна вытворная
. Аналагічна вытворная
![]() -га парадку
вызначаецца праз вытворную функцыі
-га парадку
вызначаецца праз вытворную функцыі ![]() .
Такім чынам,
.
Такім чынам, ![]() ,
, ![]() = 2, 3, … .
= 2, 3, … .
Пры вылічэнні вытворных вышэйшых парадкаў часта карыстаюцца наступнымі формуламі:
![]() ;
(3.10)
;
(3.10)
![]() ;
(3.11)
;
(3.11)
![]() ;
;
![]() ;
; ![]() .
.
Калі функцыі ![]() і
і ![]() маюць вытворныя да
маюць вытворныя да ![]() -га парадку, то
-га парадку, то
![]() ;
; ![]() ;
;
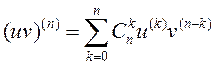 . (3.12)
. (3.12)
Формулу (3.12) называюць формулай Ляйбніца.
Дыферэнцыялы вышэйшых парадкаў вызначаюцца таксама рэку-рэнтна: ![]() . Калі зменная
. Калі зменная ![]() незалежная, то
незалежная, то
![]() .
.
Прыклад 1. Знайсці ![]() функцыі
функцыі ![]() .
.
► Паводле формулы Ляйбніца маем
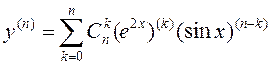 . (3.13)
. (3.13)
З (3.10) і (3.11) знаходзім, што
![]() ,
, ![]() . (3.14)
. (3.14)
Падставім (3.14) у
(3.13), атрымаем 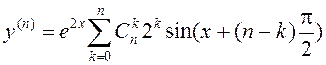 .◄
.◄
Прыклад 2. Знайсці ![]() для функцыі
для функцыі ![]() , зададзенай парамет-рычна
, зададзенай парамет-рычна ![]() ,
, ![]() ,
, ![]() .
.
► Першы спосаб. Паводле формулы (3.2) маем
![]() .
(3.15)
.
(3.15)
Прадыферэнцуем
абедзве часткі (3.15) па ![]() , атрымаем:
, атрымаем: 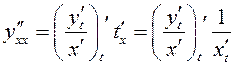 . Гэта значыць, што
. Гэта значыць, што
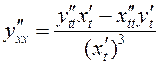 .
(3.16)
.
(3.16)
Спачатку знаходзім
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (3.17)
. (3.17)
Падставім (3.17) у (3.16). Маем
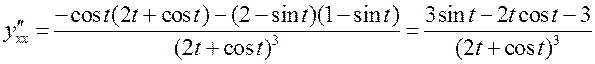 .
.
Другі спосаб. Вытворную ![]() можна таксама задать параметрычна:
можна таксама задать параметрычна:
![]() . Тады вытворную
. Тады вытворную ![]() зноў знахо-дзім паводле формулы (3.2):
зноў знахо-дзім паводле формулы (3.2):
![]() =
=
![]() .◄
.◄
Прыклад 3. Знайсці ![]() , калі
, калі ![]() і
і ![]() ,
, ![]() ,
, ![]() ,
, ![]() – вядомыя.
– вядомыя.
►Знойдзем спачатку ![]() . Затым
. Затым ![]()
![]() . ◄
. ◄
Прыклад 4. Знайсці ![]() функцыі
функцыі ![]() ,
, ![]() , зададзенай
няяў-на, калі
, зададзенай
няяў-на, калі ![]() –
незалежная зменная:
–
незалежная зменная:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.