Дыферэнцыяльнае злiчэнне функцый адной зменнай. Вытворная. Формулы i правiлы вылiчэння вытворных, страница 4

3.50.  Па парабале  рухаецца пункт так, што яго абцыса мяняецца ў залежнасці ад часу  паводле закону  ( – у секундах ,  – у метрах). Якая хуткасць змянення ардынаты ў пункце ?

3.51.  Па кубічнай парабале  рухаецца пункт так, што яго ардыната мяняецца ў залежнасці ад часу  паводле закону . Якая хуткацсь змянення абцысы ў залежнасці ад часу?

3.52.  Колькасць электрычнасці  (у кулонах ), якая працякае праз папярэчнае сячэнне правадніка, мяняецца паводле закона . Знайдзіце сілу току ў канцы пятай секунды.

3.53.  Цела з масай  = 1,5 кг рухаецца прамалінейна паводле закону  ( – у метрах). Знайдзіце кінетычную энэргію цела праз 2 с пасля пачатку руху.

3.54.  Кола круціцца так, што вугал павароту прапарцыйны квадрату часу. Першы аварот быў зроблены за 8 с. Знайдзіце вуглавую хуткасць праз 64 с пасля пачатку руху.

3.55.  Па восі  рухаюцца два пункты, якія маюць законы руху  і     ( – у секундах,  – у метрах). З якой хуткасцю аддаляюцца яны адзін ад аднаго ў момант іх сустрэчы?

3.56.  Маса  радыёактыўнага рэчыва за кошт натуральнага распаду змяняецца паводле закону , дзе  – час,  – маса ў момант часу ,  – перыяд паўраспаду. Дакажыце, што хуткасць распаду радыёактыўнага рэчыва ў кожны момант часу прапарцыйная колькасці рэчыва ў гэты момант. Знайдзіце каэфіцыент прапарцыйнасці.

3.57.  Цягнік і паветраны шар адпраўляюцца адначасова з аднаго пункта. Цягнік рухаецца раўнамерна з хуткасцю 50 , шар падымаецца (таксама раўнамерна) з хуткасцю 10 . З якой хуткасцю яны аддаляюцца адзін ад другога?

3.58.  Конь бяжыць па акружыне з хуткасцю 20 . У цэнтры акружыны знаходзіцца ліхтар, а на датычнай да акружыны ў пункце, адкуль конь пачынае бег, пабудавана агароджа. З якой хуткасцю будзе рухацца цень каня ўздоўж агароджы ў момант, калі конь прабяжыць   акружыны?

3.3. ДЫФЕРЭНЦЫЯЛ ФУНКЦЫІ

Функцыя  называецца дыферэнцавальнай у пункце , калі яе прырост  у гэтым пункце можна запісаць у выглядзе

,                                (3.5)

дзе А не залежыць ад , а  ёсць бясконца малая і непарыўная ў пункце   функцыя (). Для дыферэнцавальнасці функцыі  у пункце  неабходна і дастаткова існаванне ў гэтым пункце вытворнай  . Пры гэтым .

Дыферэнцыялам дыферэнцавальнай функцыі ў пункце  называюць лінейную частку яе прыросту ў гэтым пункце, г. зн. функцыю ад 

         .                                            (3.6)

Дыферэнцыялам незалежнай зменнай  будзем называць прырост гэтай зменнай: . Тады формула (3.6) набывае канчатковы выгляд:

         .                                          (3.7)

Для набліжанага вылічэння значэння функцыі ў пункце  можна карыстацца формулай

          .                              (3.8)

УЛАСЦІВАСЦІ ДЫФЕРЭНЦЫЯЛА

Для ўсіх дыферэнцавальных функцый  і  праўдзяцца роўнасці

;                  , ;           ;                    .

Інварыянтнасць формы першага дыферэнцыяла: формула (3.7) праўдзіца і ў тым выпадку, калі  з’яўляецца не незалежнай зменнай, а функцыяй.

Прыклад 1. Знайсці дыферэнцыял функцыі  у пункце .

►Першы спосаб. Спачатку знаходзім прырост функцыі ў гэтым пункце:

Лінейная частка  будзе роўная , таму .

Другі спосаб. На падставе формулы (3.7)

. ◄

Прыклад 2. Карыстаючыся ўласцівасцямі першага дыферэнцыяла, знайсці  у пункце  для функцыі , якая зададзена няяўна з дапамогай раўнання

.                                               (3.9)

►Знойдзем дыферэнцыял ад левай часткі (3.9) з дапамогай уласці-васцяў дыферэнцыяла:

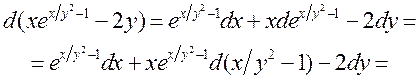
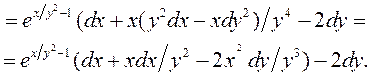
Калі  = 4, а  у= 2, то . Дыферэнцыял ад правай часткі (3.9) у кожным  пункце будзе роўны 0, таму і дыферэнцыял ад яе левай часткі таксама роўны 0, і мы атрымліваем: калі  = 4, у = 0, то , адкуль вынікае .◄

Прыклад 2. Замяняючы прырост функцыі яе дыферэнцыялам, знайсці .

►Каб пры карыстанні формулай (3.8) памылка была найменшай, зной-дзем найбліжэйшы да  пункт , у якім значэнне функцыі можна вылічыць дакладна. У нашым прыкладзе  ў  якасці  такога  пункта  можна