Измерение концентрации. Измерения в химическом анализе. Концентрация. Правильность результатов химического анализа, страница 15

* Погрешность измерения — отклонение результата измерения от действительного (истинного) значения измеряемой величины.

Необходимость в объяснении термина "погрешность измерения" вызвана тем, что в предыдущих главах учебника он не встречался. По­явление его в гл. 6 объясняется различием в концептуальных подходах к теории точности измерении автора учебника И.Ф. Шишкина и Ю.И. Александрова, написавшего данную главу. Это отражает те тенден­ции в развитии метрологии, которые существуют на сегодняшний день;

одна из них сложилась давно и закреплена в многочисленных норматив­ных документах ГСИ (именно ее и придерживался Ю.И. Александров), другая, из которой исходил И.Ф. Шишкин, избавляет науку об измере­ниях от излишней зарегламентированности и открывает широкую воз­можность проникновения ее методов в другие науки и сферы деятель­ности человека. — Примеч. ред.)

Когда оценка s² производится из результатов градуировочных экспериментов, используют уравнение

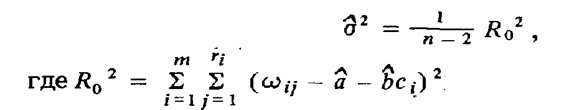
Погрешность измеряемого сигнала (w_c⁰) в предположе­нии о нормальном распределении экспериментальных данных оценивается в виде:

                                                                                         (49)

где В = Z_1-g/2 [v/c²_{v, a} ] ; c_{v, a/2} — нижний квантиль c² — распределения с v степенями свободы; ² — оценка диспер­сии s² при v степенях свободы.

Таким образом, оценка случайной погрешности искомой концентрации () может быть произведена одним из следую­щих способов.

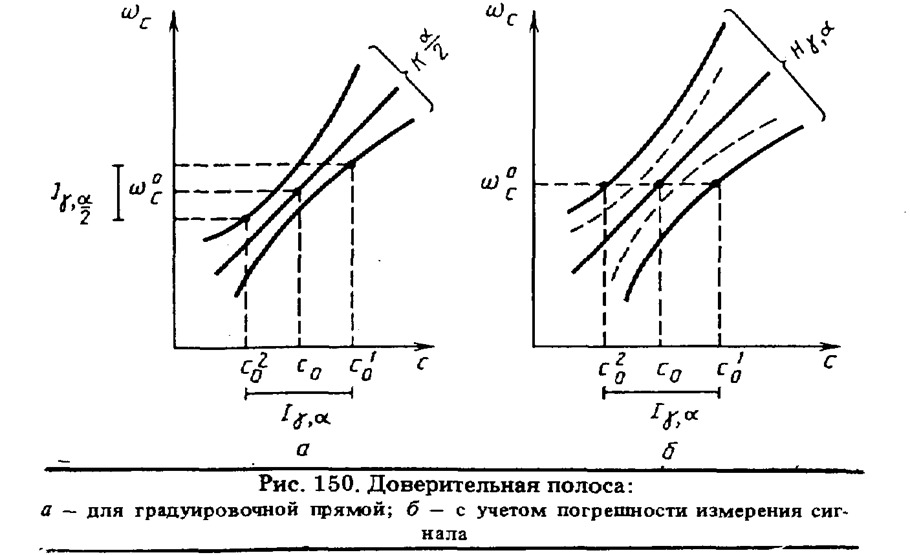
1 способ. В этом случае используют результаты оценки доверительной полосы градуировочной прямой (рис. 150, а). На оси ординат откладывается среднее значение измеренного сигнала () и его оценка в виде I_g,a . Проекции соот­ветствующих им точек пересечения с нижней и верхней гра­ницей доверительной полосы градуировочной прямой на ось абсцисс позволяют найти максимальное (c₀²) и минималь­ное (с₀¹) значения концентрации, определяющие интерваль­ную оценку концентрации , соответствующей среднему значению . Если бы градуировочная прямая была извест­на точно, то погрешность определения  была бы обуслов­лена только погрешностью измерения  и соответствова­ла бы интервалу, заключенному между пунктирными пря­мыми.

2 способ. В этом случае погрешность измерения  учи­тывают непосредственно в виде оценки Нg,a определяемой как

Нg,a = [A(c)+ B/ ]   (50)

H_ откладывают в виде доверительной полосы на градуировочном графике (см. рис. 150, б). Оценка погреш­ности определения концентрации производится в резуль­тате проекции на ось абсцисс точек пересечения горизон­тальной прямой, отвечающей среднему значению измеряе­мого сигнала () с верхней и нижней границами Нg,a Дан­ный способ наиболее пригоден, когда число параллельных определений (k) при анализе неизвестной пробы всегда оди­наково.

Интервал I_g,a  следует рассматривать как интервал значе­ний концентраций  , при которых пробам с этими концентра­циями соответствует с вероятностью (1 — g) диапазон изме­ряемых значений со средним значением .

Данный подход к оценке погрешности измерения концен­трации позволяет дать определения таким понятиям как:

1. Предел обнаружения, относящийся к измеряемому аналитическому сигналу, w_min (Limit of Decision);

2. Предел обнаружения, относящийся к концентрации, c_min (Limit of Detection);

3. Нижняя граница определяемых концентраций (c_опр. ) (Limit of Determination).

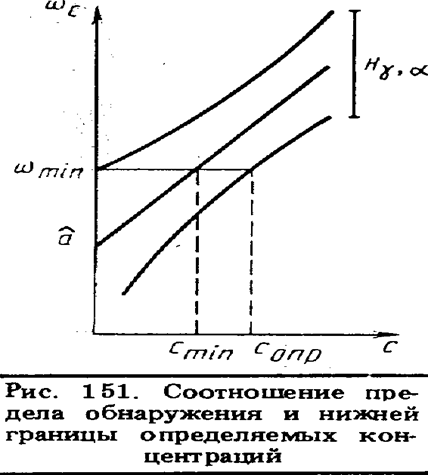
Пределом обнаружения как измеряемого аналитического сигнала, так и концентрации называют минимальное значение сигнала концентрации, которое может быть установлено с заданной доверительной вероятностью.

Предел обнаружения w_min пред­ставляет верхнее значение Нg,a,  установленное для холостого опы­та (с = 0) и на рис. 151 изображен в виде отрезка на оси ординат. Значение w_min определяют, ис­пользуя   градуировочное  урав­нение (46), также уравнения (48) и (50):

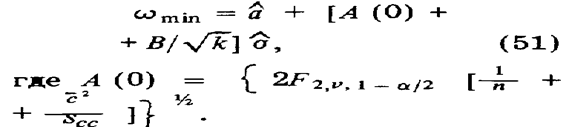
Предел обнаружения с mm оп­ределяют с учетом уравнений (51) и (47):

                                                      c_min = (w_min –  )/   .                                                             (52)

На рис. 151 показано, что графически с nun соответствует отрезок на оси абсцисс, получаемый как проекция на эту ось точки пересечения горизонтальной прямой, отвечающей w_min с градуировочной прямой.

Нижняя граница определяемых концентраций (с_опр) представляет минимальное значение концентрации, для ко­торого с уровнем значимости (1 — a) и с вероятностью не менее (1 — g/2) результат измерения сигнала будет боль­ше, чем предел его обнаружения (w_min ) На рис. 151 c_опр соответствует отрезок на оси абсцисс, получаемый как проек­ция на эту ось точки пересечения горизонтальной прямой, отвечающей w_min нижней границей Н_g,a.

Важно отметить, что приведенные выше способы нахож­дения w_min ,c_min , c_опр связаны с введением каких-либо конкретных коэффициентов типа Зs или 6s.

Широко распространена точка зрения, что проведение на этапе пробоподготовки концентрирования позволяет уменьшить нижнюю границу определяемых концентраций. Представленное на рис. 151 соотношение показывает ошибоч­ность такого заключения (с_опр зависит только от чувстви­тельности метода измерения и метрологических характерис­тик используемых при этом средств измерений).

Прежде чем перейти к следующему разделу, где будут рас­смотрены способы контроля правильности результатов хими­ческого анализа, необходимо сделать краткие выводы.

Выше бьет изложен подход к обеспечению единства изме­рений концентрации от проблем воспроизведения единиц концентрации, с учетом особенностей концентрации как физи­ческой величины, до вопросов передачи размера единиц кон­центрации в результате проведения градуировки.

Необходимо еще раз подчеркнуть, что независимо от того, какая система передачи размера единиц применяется для обес­печения единства измерений — децентрализованная или центра­лизованная, используемые для передачи размера единиц сред­ства измерений всегда выполняют функцию образцовых средств измерений, к которым и относят образцовые меры.