Градуировка универсальных приборов, предназначенных для проведения количественного анализа, осуществляется в два этапа. На первом этапе производится передача размеров единиц тех физических величин, которые используются в дальнейшем для определения концентрации (обычная градуировка) . Для ее проведения используются эталоны и исходные образцовые меры единиц физических величин (см. разд. 6.1). На втором этапе определяется уравнение связи в виде градуировочной характеристики. Для этой цели используются образцовые меры концентрации, являющиеся аналогами наборов образцовых мер. Эти образцовые меры концентрации представляют собой смеси с известными по методу приготовления значениями концентрации компонентов в установленном диапазоне, получаемые из исходных образцовых веществ.
Таким образом, градуировка универсальных приборов производится с использованием двух видов мер: мер физических свойств, измерение которых положено в основу аналитического метода, и мер концентрации. Градуировка по мерам данной физической величины позволяет использовать универсальный прибор для количественного анализа не одного вещества, а целого их ряда, в связи с чем необходима дополнительная градуировка по образцовым мерам концентрации остальных компонентов.
Отличие анализаторов состава заключается в том, что для них уравнение связи в явном виде не устанавливается. Поэтому для этой группы приборов отпадает необходимость проводить измерения действительных значений физических свойств, т. е. отпадает необходимость в градуировке по первой группе мер. Основное требование, предъявляемое к анализаторам состава, заключается в стабильности их показаний. Поэтому градуировка анализаторов состава производится только по образцовым мерам концентрации для нанесения шкалы концентрации. Типичным представителем данной группы шкальных приборов являются газоанализаторы. Измерения концентрации на приборах данной группы осуществляются в виде прямых отсчетов показаний шкалы. Недостатком данной группы приборов является жестко ограниченная узкая область применения.
Рассмотрим более подробно установление уравнений связи, представленных в общем виде уравнениями (39) и (40) . Для практического их использования они могут быть преобразованы в таблицы, графики и в функциональные уравнения.
Примерами таблиц являются таблицы спектральных линий в широком диапазоне длин волн, таблицы молекулярных спектров. Наиболее широкое употребление данная форма имеет при проведении качественного анализа.
В то же время графическое представление градуировочных функций преимущественно используется в количественном анализе. При этом, как правило, стремятся привести эту функцию к линейной. Для этого применяют различные математические преобразования, в частности, логарифмирование. В последнем случае при графическом изображении используют диаграммы с логарифмическими или полулогарифмическими координатами.
Наиболее точную градуировочную характеристику получают в третьем случае, когда эта характеристика выражается в аналитическом виде как полином третьей, реже четвертой степени.
Независимо от формы представления градуировочной характеристики (аналитической или графической) значения концентрации (сi), используемые при этом, рассматриваются как детерминированные величины. Это требует, в свою очередь, чтобы эти значения концентрации были известны с точностью, по крайней мере, в три раза превышающей точность измерения физического свойства, используемого в дальнейшем для нахождения аналитической функции данного метода.
Рассмотрим наиболее типичный случай, когда градуировочная функция может быть представлена в виде линейной:
wc=а +Ьс, (45)
где с — концентрация, которая может быть выражена в любых ее единицах.
Используя набор образцовых мер, представляющий ряд (т) значений концентрации (сi) во всем диапазоне измерений данным методом (cH – сK) и проведя для каждой меры ri параллельных измерений wi,c , получим
m
п = åri пар (сi ; wi,c),
i=1
которые позволяют установить конкретное линейное уравнение.
Обычно конкретные значения коэффициентов ![]() и
и ![]() в уравнении (45) определяют методом наименьших
квадратов.
в уравнении (45) определяют методом наименьших
квадратов.
Эмпирическая градуировочная прямая будет
![]() (46)
(46)
Проведение изложенной выше градуировки представляет собой только предварительный этап. При измерении концентрации приходится решать обратную задачу: для измеренного конкретного физического свойства (wc0) аналитической пробы следует установить соответствующее ему значение концентрации (с0) и оценить погрешность этого значения*.
Искомое значение концентрации (![]() ) определяется из уравнения
градуировочной прямой _
) определяется из уравнения
градуировочной прямой _
![]() (47)
(47)
Для оценки случайной погрешности определения искомой
концентрации (![]() ) необходимо учесть:
) необходимо учесть:
1) погрешность градуировочной прямой;
2) погрешность измеряемого сигнала (wc0 ).
Погрешиость градуировочной прямой целесообразно оценивать не в виде
доверительных границ для каждой экспериментальной точки, используемой для
установления градуировочной функции, а в виде доверительной полосы при заданном
уровне значимости (1 — а/2)
для всего рабочего интервала концентраций (cH . . . сK), как это показано на рис. 150. Оценка ширины
доверительной полосы А (с) ![]() производится по
уравнению
производится по
уравнению
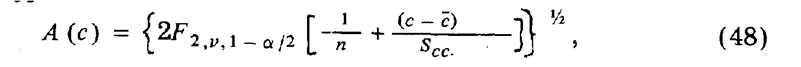
где F 2, v , 1 – а/2 — квантиль F-распределения с (2, v)
степенями свободы; ![]() , -- среднее
значение и границы разброса измеренных значений сi в эксперименте по градуировке,
, -- среднее
значение и границы разброса измеренных значений сi в эксперименте по градуировке,
определяемые
согласно 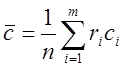 ;
; 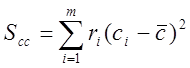
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.