4. Допускаемые напряжения при изгибе:
![]() пр =
пр =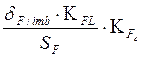 .
.
По табл. 9.8
![]() для шестерни и колеса :
для шестерни и колеса :
![]() МПа
МПа
![]() = НВ + 260 = 210 + 260 =470 Мпа ,
где
= НВ + 260 = 210 + 260 =470 Мпа ,
где
S![]() - коэффициент безопасности;
- коэффициент безопасности;
![]() - коэффициент долговечности;
- коэффициент долговечности;
![]() - коэффициент, учитывающий влияние
реверсивной нагрузки
- коэффициент, учитывающий влияние
реверсивной нагрузки
Тогда допускаемые напряжения при изгибе :
·
для шестерни ![]()
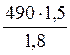
![]() Мпа
Мпа
![]() =
=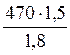
![]() Мпа
Мпа
5. Передаточное число:
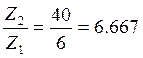
6. Внешний делительный диаметр большого конического колеса определяем по формуле:
d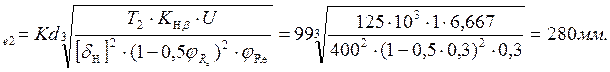 , где
, где
Kd = 99 - числовой коэффициент для прямозубых передач.
Т![]() - вращающийся момент на колесе, Н
- вращающийся момент на колесе, Н![]()
![]() - коэффициент, зависящий от
- коэффициент, зависящий от ![]() j
j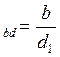 ,
где b – ширина зубчатого венца, мм.
,
где b – ширина зубчатого венца, мм.
d![]() - диаметр делительной окружности шестерни.
- диаметр делительной окружности шестерни.
![]() - коэффициент длины зуба.
- коэффициент длины зуба.
7. Внешний окружной модуль.
m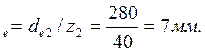
8. Конусное расстояние
R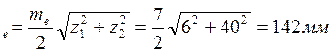
9. Длина зуба или ширина зубчатого венца:
b = ![]()
![]()
Принимаем b=45 мм.
10. Внешний делительный диаметр шестерни:
d![]() =
m
=
m![]() мм.
мм.
11. Углы при вершинах начальных конусов :
Ctg ![]()
![]() °10¢
°10¢
![]() =
90° - 8°10¢ = 81°50¢
=
90° - 8°10¢ = 81°50¢
12. Средний делительный диаметр шестерни:
d![]() Re
– 0,5
Re
– 0,5![]() °10¢ = 33,9 мм.
°10¢ = 33,9 мм.
13. Средний окружной модуль:
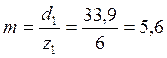 мм.
мм.
14. Выполняем проверочный расчет на усталость по контактным напряжениям.
Для сохранения методики проверочного расчета, рекомендованной ГОСТ 21354 – 75
для цилиндрицеских передач, заменим конечное колесо условным цилиндрическим с
диаметром d![]() и шириной
венца b ( рис. ).
и шириной
венца b ( рис. ).
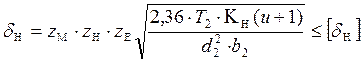 , где
, где
z![]() ; z
; z![]() ; z
; z![]() ;
; ![]()
![]()
![]() ;
;
![]() ( по таблице 9,11
( по таблице 9,11 ![]() )
)
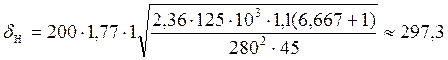 Мпа , т.е.
Мпа , т.е.
![]() МП больше чем
МП больше чем ![]() Мпа.
Мпа.
15. Определяем основные размеры шестерни и колеса:
Диаметры вершин
зубьев ( см. рис. 9.10 ![]() )
)
da![]() °10¢ = 55,8 мм.
°10¢ = 55,8 мм.
da![]() °50¢ = 281,9 мм.
°50¢ = 281,9 мм.
Диаметры впадин зубьев:
d![]()
![]() мм.
мм.
d![]() 50¢ = 277,5 мм.
50¢ = 277,5 мм.![]()
16. По таблице 9.9![]() для прямых зубьев колес
конической передачи при твердости стали
менее 350 НВ можно принять 9-ю степень точности, но для уменьшения динамической
нагрузки вместо наименьшей допустимой, выбираем 8-ю степень точности.
для прямых зубьев колес
конической передачи при твердости стали
менее 350 НВ можно принять 9-ю степень точности, но для уменьшения динамической
нагрузки вместо наименьшей допустимой, выбираем 8-ю степень точности.
1- центральное солнечное колесо
2- сателлиты
3- центральное корончатое колесо
Рисунок. Расположение сателлитов в корончатом колесе.
1. Передаточное отношение редуктора:
i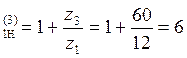 , где
, где
z![]() - число зубьев корончатого колеса
- число зубьев корончатого колеса
z![]() - число зубьев солнечного колеса.
- число зубьев солнечного колеса.
2. Число зубьев сателлита:
z![]()
3. Принимаем число сателлитов n![]() и проверяем условия собираемости:
и проверяем условия собираемости:
а) условия соосности
не проверяю т.к. z![]() находил
из этого условия;
находил
из этого условия;
б) условие вхождения зубьев в зацепление при n![]() и равных центральных
углах расположения сателлитов:
и равных центральных
углах расположения сателлитов:
( z![]() ) / n
) / n![]() целое число
целое число
( 12 + 60 ) / 3 = 24;
в) условие соседства:
(х![]() (z
(z![]()
(12 + 24 ) ![]()
31,2>26,5
так как условия
собираемости сошлись, то окончательно принимаем ![]() n
n![]() .
.
4. С учетом технологических возможностей предприятия-изготовителя выбираем для всех колес сталь 40 ХН улучшенную, твердостью 295 НВ.
Предел контактной выносливости:
![]() Мпа.
Мпа.
Допускаемые контактные напряжения:
![]() Мпа.
Мпа.
5. Межосевое расстояние передачи:
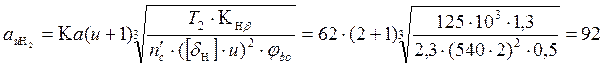 мм. , где
мм. , где
u = z![]() / z
/ z![]() =24 / 12 = 2 -
передаточное число равное отношению числа зубьев большего колеса,
рассчитываемой пары к меньшему ( u =
=24 / 12 = 2 -
передаточное число равное отношению числа зубьев большего колеса,
рассчитываемой пары к меньшему ( u = ![]() )
)
T![]() - вращающийся момент, действующий на большое колесо, Н мм.
- вращающийся момент, действующий на большое колесо, Н мм.
n¢![]()
![]() ( см. таблицу 9.11
( см. таблицу 9.11 ![]() ).
).
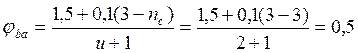 - коэффициент ширины венца колеса.
- коэффициент ширины венца колеса.
6. Модуль зацепления:
M=2a![]()
![]() мм.
мм.
7. Делительные диаметры колес:
d![]() мм.
мм.
d![]()
![]() мм.
мм.
d![]()
![]() мм.
мм.
8. Ширина колес:
b = ![]() мм.
мм.
9. Проверяем прочность зубьев на изгиб по формуле:
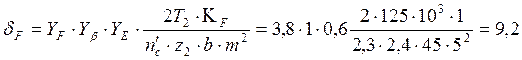 Мпа.
Мпа.
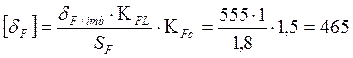 Мпа - допускаемые напряжения на
изгиб, где
Мпа - допускаемые напряжения на
изгиб, где ![]() Мпа.
Мпа.
![]() , 9,2 < 465.
, 9,2 < 465.
Проверка сошлась.
Вал натяжной станции работает на изгиб ( рис. ). Сила, действующая на вал натяжной станции во время работы конвейера, зависит от статических натяжений цепей в точках 2 и 3 (см. рис. ) и находится по формуле:
P![]() кН. , где
кН. , где
P![]() и P
и P![]() - силы
натяжения цепей, кН.
- силы
натяжения цепей, кН.
![]() - коэффициент запаса прочности на
изгиб.
- коэффициент запаса прочности на
изгиб.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.