Взаимосвязь между извлечениями компонентов и сепарационными характеристиками схем. Методы и формулы для вычисления абсолютных сепарационных характеристики схем и их частей, страница 8

Представляет интерес анализ циркулирующих нагрузок для симметричных схем (флотационных и других) интерес. До сих пор речь шла в основном о , теперь  рассмотрим  на примере симметричных схем флотации, начнем с анализа циркулирующих нагрузок схемы П = К = 1. Если для всех операций симметричной схемы флотации характеристики одинаковы, т. е. если одинаковы произведения , то схема в целом является «сбалансированной», и ее результирующая сепарационная характеристика имеет флотируемость разделения  и крутизну ;  наиболее близка к идеальному ступенчатому закону . Если же функции  для отдельных операций не одинаковы (т.е. величины Sи t_ф отклоняются от среднего значения), то симметричная схема становится «несбалансированной».  В результате этого  сильнее отклоняется от , а циркулирующие нагрузки отклоняются от нормы.

Сепарационные характеристики и для циркулирующих нагрузок (продукты и q₆на рис. 6. 1, г) имеют согласно формулам (6.7), следующий вид:

; ,                                       (6.17)

где  берется по формуле (6.8). Для общности анализа в дальнейшем величину  в основной операции обозначим через х, т.е. для основной операции флотации берем . Если во всех операциях одинаковы (сбалансированный режим), то имеем . Подставив эти в формулы (6.8) и (6.17), получим формулы  для сбалансированного режима. По этим (опущенным здесь) формулам на рис. 6.3, а построены соответствующие графики (расчеты сделаны компьютером).

Если время флотации в перечистной и контрольной операциях схемы, показанной на рис. 5.1,г, увеличить, например, вдвое, то получим (несбалансированный режим) ; . Теперь ,  и  для этой схемы изменятся так, как показано на рис. 6.3,б. Если время перечистной флотации будет вдвое больше, а контрольной – вдвое меньше, чем основной, то получим ; ; . Соответствующие графики , ,  показаны на рис. 6.3, в. На рис. 6.3, г, д показаны графики для других несбалансированных режимов схемы, представленной на рис. 6. 1,  г.

Графики, представленные на рис. 6.3, позволяют сделать следующие выводы. В сбалансированном режиме (см. рис. 6.3, а) оба циркулирующих потока ;  идентичны по фракционному составу, причем в них максимально извлекаются минеральные частицы с флотируемостью k, равной флотируемости разделения ,  которая находится из графиков  по уравнению ; в концентрат q₄сепарируются преимущественно частицы с флотируемостью k> k_p, на что указывает график .

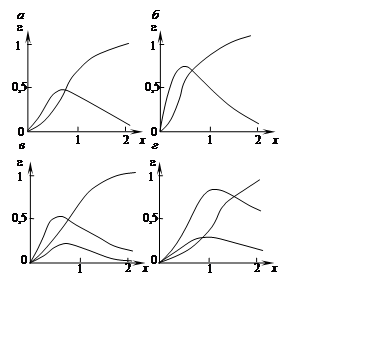
Рис. 6.3. Сепарационные характеристики простой симметричной схемы флотации

При одновременном увеличении фронтов перечисткой и контрольной операций (см. рис.6.3,б) циркулирующие потоки становятся различными, причем q₆(k) > q₅(k) для любой фракции флотируемости   при , любом исходном питании . Наоборот, при уменьшении фронтов перечистной и контрольной операции (см. рис. 6.3, г) получается . Оба циркулирующих потока существенно возрастают при уменьшении фронта перечистки и увеличении фронта контрольной флотации (рис. 6.3, д). Во всех несбалансированных режимах (рис. 6.3, б-д) график больше отклоняется от идеальной ступенчатой характеристики , чем для сбалансированного режима (рис. 6.3, а). Подобный анализ для схем, в которых П = К = 2, выявляет резкое увеличение циркулирующих потоков  и при уменьшении фронтов перечистных и увеличении фронтов контрольных операций по сравнению с фронтом основной операции; циркулирующие потоки от II перечистной и II контрольной операций колеблются меньше.

Для схем, в которых П = К = 2, анализ опустим, приведем только исходные формулы для . Для канонической схемы П = К = 2 (см. рис. 6.1, д): циркуляция от I-ой перечистной и I-ой контрольной операций: ; . Циркуляция от II-ой перечистной и II-ой контрольной: ; .

Для полуканонической схемы  П = К = 2 (рис. 6.1, е) циркуляция от I-ой перечистной и I-ой контрольной операций ; ; циркуляция от II-ой перечистной и II-ой контрольной операций: ; .