Взаимосвязь между извлечениями компонентов и сепарационными характеристиками схем. Методы и формулы для вычисления абсолютных сепарационных характеристики схем и их частей, страница 7

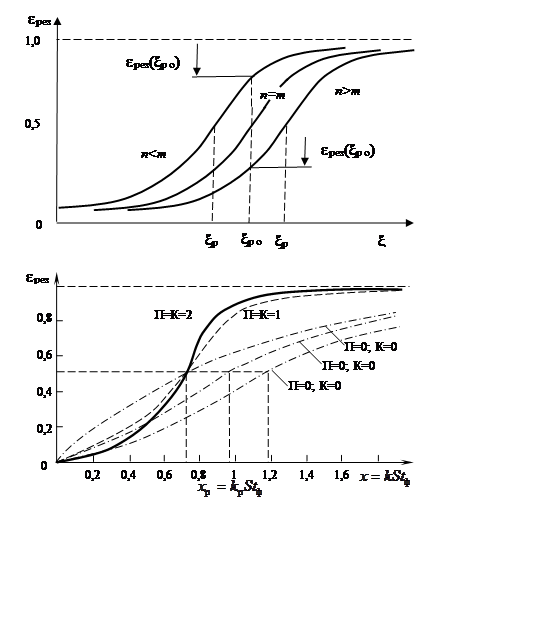
Рис.  6.2. Результирующие сепарационные характеристики флотационных схем.

6.4. Примеры анализа результирующих сепарационных характеристик гравитационных, магнитных, флотационных и других схем

Рассмотрим примеры вычисления абсолютных результирующих сепарационных характеристик схем. Пример 1,а. Для гравитационной схемы с одной перечистной операцией П = 1, К = 0 и частными сепарационными характеристиками операций для отсадочных машин или тяжелосредных сепараторов в виде: 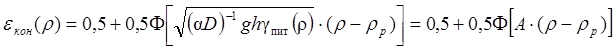 по формуле (6.8) получаем: ; где 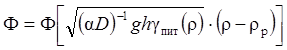. Окончательно можно рассчитать при численном задании всех параметров, в частности: ; .

Пример 1,б. Для гравитационной схемы с одной перечистной П = 1 и одной контрольной К = 1 операциями и частными сепарационными характеристиками операций для отсадочных машин (или тяжелосредных сепараторов) в виде гиперболического тангенса: 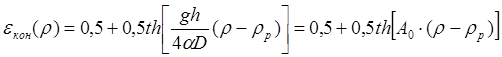 по формуле (6.8) получаем: .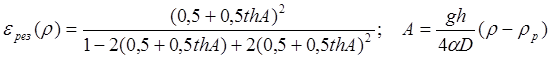

Пример 2,а. Для симметричной флотационной схемы с одной перечисткой П = 1 и одной контрольной К = 1 операциями с идентичными сепарационными характеристиками       , по формулам (6.8) или (6.10) получаем: 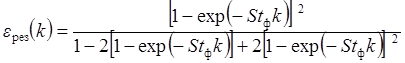      . Конкретные параметры могут иметь следующие значения: удельная поверхность раздела фаз S = 800 м²/м³; время флотации .

Пример 2,б. Для симметричной разветвленной флотационной схемы с пятью перечистными П = 5 и пятью контрольными К = 5 операциями с идентичными сепарационными характеристиками  , по формулам (6.8) или (6.10) получаем: .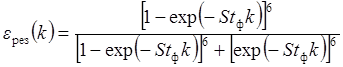

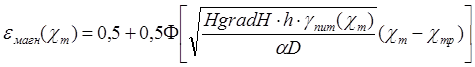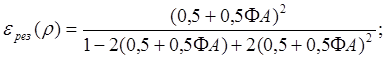Пример 3. Для схемы магнитного обогащения (П = К = 1) с идентичными характеристиками операций  по формулам (6.8) или (6.10) получаем: где 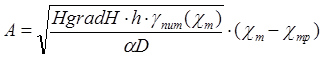                    . Из этих примеров ясно, как можно получить абсолютные сепарационные характеристики конкретных схем обогащения.

Перейдем к примерам анализа графиков и главных параметров  и  для  результирующих  сепарационных  характеристик схем.  Граница разделения схемы и крутизна сепарационной характеристики  схемы могут быть вычислены графически или аналитически. График или таблица сепарационной характеристики ,  вычисляется «вручную» или с помощью ЭВМ в дискретных точках интересующего диапазона , в частности,, , ,  и т. д.  График или таблица  могут быть построены и по исходным экспериментальным данным, , , также представленным графиками или таблицами.

На рис. 6.2 показаны  для нескольких флотационных схем, причем для простоты в этих примерах взяты одинаковые сепарационные характеристики в операциях , . Из графиков  для флотацион ных схем, приведенных на рис. 6.2, в случаях симметричных схем (, и ) получается одно и то же значение флотируемости разделения:      . Для несимметричной схемы (, ) имеем , а для схемы ,  получаем . Крутизна  вычисляется после нахождения  по формуле .Это всегда можно сделать по аналитической формуле для  либо графическим дифференцированием по тангенсу угла наклона касательной к  в рабочей точке.

Например, для флотационной схемы П = К = 1 с  полученной выше при  получаем , а для симметричной флотационной схемы (П = К = 2) получаем . Для одной операции флотации (П = К = 0)  эта крутизна равна . Видим, в частности, что по мере увеличения числа перечистных и контрольных операций крутизна растет, т. е. приближается к идеальной ступенчатой функции.

6.5. Анализ абсолютных сепарационных характеристик для циркулирующих  и других внутренних продуктов схем

Абсолютные сепарационные характеристики для циркулирующих и других внутренних продуктов схем  отличаются от результирующих сепарационных характеристик . Сразу отметим общее в этих различиях. Результирующие сепарационные характеристики  имеют графики похожие на сглаженную ступень, изменяющиеся от нуля до единицы по вертикали. Абсолютные сепарационные характеристики для циркулирующих и других внутренних продуктов схем  имеют ‘горбатые’ графики с максимумом в области границы разделения схемы. Эти максимумы особенно явно выражаются для циркулирующих продуктов. Физический смысл поясняется тем, что граничные фракции (между концентратными и хвостовыми) направляются схемой в оборотные потоки – на дополнительную сепарацию.