Задачами синтеза технологических схем
являются: выбор параметров сепараторов, максимизирующих
или обеспечивающих заданную крутизну![]() ; выбор наиболее простой (оптимальной)
конфигурации схемы, числа операций П и К, обеспечивающих
заданную крутизну
; выбор наиболее простой (оптимальной)
конфигурации схемы, числа операций П и К, обеспечивающих
заданную крутизну![]() , и другие. При таком подходе схема рассматривается как инструмент для
сепарации частиц сырья на продукты и влияние характеристик сырья сказывается
лишь на выборе оптимальной границы разделения ξр = ξр опт,
крутизны
, и другие. При таком подходе схема рассматривается как инструмент для
сепарации частиц сырья на продукты и влияние характеристик сырья сказывается
лишь на выборе оптимальной границы разделения ξр = ξр опт,
крутизны ![]() , параметров операций схемы. Названные и другие задачи анализа и
синтеза будут рассматриваться в последующих частях книги.
, параметров операций схемы. Названные и другие задачи анализа и
синтеза будут рассматриваться в последующих частях книги.
См.: Тихонов О. Н., Расчет схем обогащения с учетом распределения частиц минерального сырья по их физическим свойствам. Обогащение руд, 1978, № 4, с. 21—27. Тихонов О. Н., Сепарационные характеристики схем обогащения. Изв. Вузов Горный журнал, №3, 1980, с. 107-111; Тихонов О.Н., Сепарационные характеристики незамкнутых флотационных схем с ячейками из трех операций. ИВУЗ-Горный журнал №9 1979, с. 118-121.
6.2. Методы и формулы для вычисления абсолютных сепарационных характеристики схем и их частей
Абсолютные сепарационные характеристики εрез(ξ) и εi j(ξ) могут быть вычислены из частных сепарационных
характеристик операций εi(ξ). Сепарационные характеристики для конечных продуктов
схем более важны, чем для внутренних продуктов, поэтому начнем с них. Для большинства
обогатительных аппаратов частная сепарационная характеристика![]() далека
от идеальной ступенчатой; примером является флотационная машина с
экспоненциальной сепарационной характеристикой.
Именно поэтому аппараты соединяют в технологические схемы таким образом, чтобы результирующая сепарационная
характеристика
далека
от идеальной ступенчатой; примером является флотационная машина с
экспоненциальной сепарационной характеристикой.
Именно поэтому аппараты соединяют в технологические схемы таким образом, чтобы результирующая сепарационная
характеристика ![]() схемы
в целом была ближе к идеальной. Типичный путь, выработанный практикой, — эта канонические схемы. В них
имеется одна основная, П перечистных и К контрольных операций; промпродукты любой перечистной и контрольной операции возвращаются в питание предыдущей. Особенно
разветвленными являются перечистные и контрольные ветви в схемах флотации вследствие весьма неидеальной сепарационной
характеристики отдельной операции
флотации (флотационной машины).
схемы
в целом была ближе к идеальной. Типичный путь, выработанный практикой, — эта канонические схемы. В них
имеется одна основная, П перечистных и К контрольных операций; промпродукты любой перечистной и контрольной операции возвращаются в питание предыдущей. Особенно
разветвленными являются перечистные и контрольные ветви в схемах флотации вследствие весьма неидеальной сепарационной
характеристики отдельной операции
флотации (флотационной машины).
В соответствии с
общим подходом результирующей сепарационной характеристикой (двухпродуктовой)
схемы назовем отношение производительностей по элементарной
фракции ![]() в концентрате
и исходном питании:
в концентрате
и исходном питании:
![]() (6.2, а)
(6.2, а)
Производительности по элементарной фракции в концентрате и исходном питании:
![]() ;
; ![]() .
(6.2, б)
.
(6.2, б)
Знание ![]() позволяет
находить
позволяет
находить![]() также
содержание компонента в продукте
также
содержание компонента в продукте
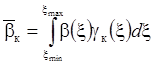 .
(6.3)
.
(6.3)
Эти формулы
получаются путем решения системы линейных алгебраических уравнений
баланса по произвольной элементарной фракции![]() для
всех продуктов схемы; число таких уравнений равно удвоенному числу
операций в схеме. Для любой i-той операции имеем два
уравнения.
для
всех продуктов схемы; число таких уравнений равно удвоенному числу
операций в схеме. Для любой i-той операции имеем два
уравнения.
![]() ;
;
![]() (6.4)
(6.4)
Первое – сумма входящих потоков
фракции ![]() равна
сумме выходящих;
равна
сумме выходящих;
второе – поток фракции в концентрате равен потоку ее в питании, умноженному на сепарационную характеристику. Последнее равенство иногда удобнее переписать в виде:
![]() (6.5)
(6.5)
Составив пары равенств для всех
операций схемы, исключив все ![]() для
внутренних промежуточных продуктов, вычислим отношение
для
внутренних промежуточных продуктов, вычислим отношение ![]() , см.
уравнение (6.2, а).
, см.
уравнение (6.2, а).
Например, для
схемы с тремя операциями (рис. 6.1,г) получим (![]() ):
):
![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
(6.6)
.
(6.6)
Система уравнений (6.6) содержит шесть линейных уравнений с шестью неизвестными; для упрощения решения можно использовать еще три равенства типа (6.5):
![]() ;
; ![]()
![]() .
.
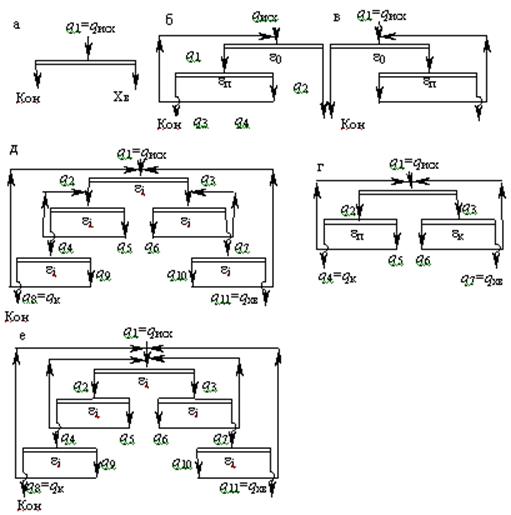
Рис. 6.1. Канонические (а-д) и полуканонические (е) схемы.
Для решения системы уравнений
(6.6) в первой и шестой строках заменим ![]() ,
в пятой заменим
,
в пятой заменим ![]() ,
при этом получим:
,
при этом получим: ![]() ;
; ![]() ;
; ![]() .
.
Подставим ![]() и
и ![]() в
первое из этих уравнений:
в
первое из этих уравнений: ![]() .
Далее найдем решение:
.
Далее найдем решение:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.