Эта формула получается из формул
(6.8) и (6.9) как частный случай при П = К = п
и ![]() . Формулы
(6.8) - (6.10) служат для вычисления абсолютных результирующих
сепарационных характеристик схем в целом
. Формулы
(6.8) - (6.10) служат для вычисления абсолютных результирующих
сепарационных характеристик схем в целом ![]() .
.
Для многих расчетов требуется знать абсолютные
сепарационные характеристики участков схемы![]() ,
, ![]() ,
, ![]() .
Выше приведена формула (6.8)
.
Выше приведена формула (6.8) ![]() , ниже дается ее расширение на
внутренние продукты схем. Для канонических
схем абсолютные сепарационные характеристики от исходного питания всей
схемы до питания основной, П перечистных и К ( контрольных операций
имеют вид:
, ниже дается ее расширение на
внутренние продукты схем. Для канонических
схем абсолютные сепарационные характеристики от исходного питания всей
схемы до питания основной, П перечистных и К ( контрольных операций
имеют вид:
![]() ;
;
![]() ;
;
![]() ;
(6.11, а)
;
(6.11, а)
где: 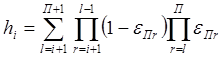 ;
; 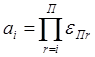 ;
; 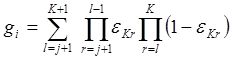 ;
; 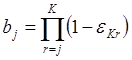 .
.
Формулы (6.11, а) являются математически точными. Они
определяют абсолютные сепарационные характеристики от исходного питания всей
схемы до питания любой i-ой операции ![]() .
От питания любой операции легко перейти к продуктам этой операции:
.
От питания любой операции легко перейти к продуктам этой операции:
![]() ;
;
![]() .
(6.11, б) где
.
(6.11, б) где ![]() есть
частная сепарационная характеристика i-ой операции по концентрату.
есть
частная сепарационная характеристика i-ой операции по концентрату.
Формулы (6.11, а) и (6.11, б) для
внутренних продуктов имеют силу и для полуканонических схем с учетом G = 1 и H = 1 (а также - для симметричных
схем). Для полуканонических схем возможно упрощение; поясним простое
мнемоническое правило ‘движения от конечного концентрата ![]() внутрь
схемы‘ при нахождении формул абсолютных сепарационных
характеристик по внутренним продуктам для полуканонических
схем. Для получения абсолютной сепарационной характеристики до питания
последней перечистки нужно известную абсолютную характеристику
внутрь
схемы‘ при нахождении формул абсолютных сепарационных
характеристик по внутренним продуктам для полуканонических
схем. Для получения абсолютной сепарационной характеристики до питания
последней перечистки нужно известную абсолютную характеристику ![]() разделить на частную
сепарационную характеристику этой последней перечистки
разделить на частную
сепарационную характеристику этой последней перечистки ![]() . Для получения абсолютной сепарационной характеристики до хвостов последней
перечистки нужно полученный результат умножить на частную характеристику по
хвостам
. Для получения абсолютной сепарационной характеристики до хвостов последней
перечистки нужно полученный результат умножить на частную характеристику по
хвостам ![]() . Для получения абсолютной сепарационной характеристики до питания
предпоследней перечистки нужно
. Для получения абсолютной сепарационной характеристики до питания
предпоследней перечистки нужно ![]() разделить на частную
сепарационную характеристику этой предпоследней перечистки
разделить на частную
сепарационную характеристику этой предпоследней перечистки ![]() . Такое
движение – от последней перечистки по часовой стрелке через основную операцию
до контрольных – позволяет сравнительно легко найти абсолютные
сепарационные характеристики для всех внутренних продуктов полуканонической
схемы, начиная от
. Такое
движение – от последней перечистки по часовой стрелке через основную операцию
до контрольных – позволяет сравнительно легко найти абсолютные
сепарационные характеристики для всех внутренних продуктов полуканонической
схемы, начиная от ![]() . Для
канонических схем рассмотренное мнемоническое правило не имеет силы.
. Для
канонических схем рассмотренное мнемоническое правило не имеет силы.
Заметим формулу (6.8) можно записать в более симметричном виде:
![]() ;
;
![]() ;
;
![]() (6.12)
(6.12)
Здесь в члене В все
частные сепарационные характеристики операций ![]() ,
, ![]() ,
, ![]() ,
которые, как было условлено, относятся к концентратам, заменены на
‘хвостовые’
,
которые, как было условлено, относятся к концентратам, заменены на
‘хвостовые’ ![]() ,
, ![]() и
и ![]() ,
которые относятся к хвостам. При такой записи члены А и
В отличаются только числами П и К. Ниже даны примеры
пользования формулами (6.8), (6.11) и (6.12)
,
которые относятся к хвостам. При такой записи члены А и
В отличаются только числами П и К. Ниже даны примеры
пользования формулами (6.8), (6.11) и (6.12)
Пример 1. По формулам (6.8), (6.11) и
(6.12) для схемы, содержащей одну основную и одну перечистную ((П = 1, К = 0)
операции получаем
результирующую сепарационную характеристику: 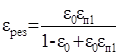 .
Для концентрата основной операции (чернового):
.
Для концентрата основной операции (чернового): 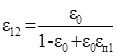 .
Для хвостов основной операции:
.
Для хвостов основной операции: 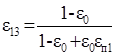 .
.
Пример 2. По формулам (6.8) и (6.12) для
схемы, содержащей
одну основную, одну перечистную (П = 1) и одну контрольную (К = 1) операции получаем результирующую характеристику: 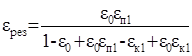 .
Для концентрата основной операции:
.
Для концентрата основной операции: 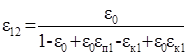 .
Для хвостов перечистки (оборотный продукт):
.
Для хвостов перечистки (оборотный продукт): 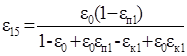 .
Для концентрата контрольной операции:
.
Для концентрата контрольной операции: 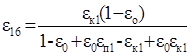 .
.
Пример 3. Для схемы с двумя перечистными (П = 2) одной
контрольной (К = 1) операциями: 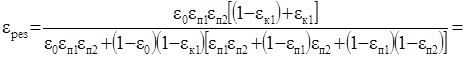
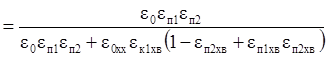 .
Для концентрата основной операции (чернового):
.
Для концентрата основной операции (чернового):
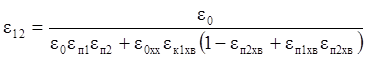 .
Для концентрата первой перечистки:
.
Для концентрата первой перечистки:
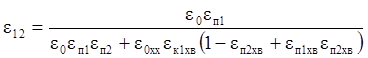 .
Для хвостов первой перечистки:
.
Для хвостов первой перечистки: 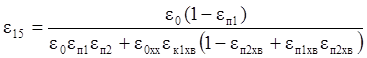 .
.
Пример 4. Аналогичным образом для
симметричной схемы П = К = 2 получаем: 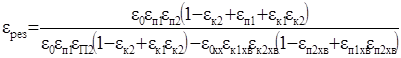 .
.
Рассмотренные
формулы для ![]() в
общем случае (при любом числе П и К) во-первых, позволяют избежать
трудоемкого решения уравнений баланса типа (6.6); во-вторых, по
ним можно сравнительно легко «подобраться» к
в
общем случае (при любом числе П и К) во-первых, позволяют избежать
трудоемкого решения уравнений баланса типа (6.6); во-вторых, по
ним можно сравнительно легко «подобраться» к ![]() для
внутренних продуктов схемы с помощью формул (6.4) и (6.5). Все формулы
справедливы не только для одномерных сепарационных характеристик
для
внутренних продуктов схемы с помощью формул (6.4) и (6.5). Все формулы
справедливы не только для одномерных сепарационных характеристик ![]() ,
, ![]() ,
, ![]() двухмерных
и многомерных
двухмерных
и многомерных ![]() ;
; ![]() ;
; ![]() ,
, ![]() ,
причем теперь прослеживается движение по схеме не одномерной
фракции
,
причем теперь прослеживается движение по схеме не одномерной
фракции ![]() , а
произвольной многомерной размером
, а
произвольной многомерной размером ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.