Другие предметы \ ТЕОРИЯ СЕПАРАЦИОННЫХ ПРОЦЕССОВ

Взаимосвязь между извлечениями компонентов и сепарационными характеристиками схем. Методы и формулы для вычисления абсолютных сепарационных характеристики схем и их частей, страница 14

Абсолютные сепарационные характеристики технологических схем и их частей  кодируются как и частные сепарационные характеристики, но с отбрасыванием UN.   Напомним: функция  есть абсолютная сепарационная характеристика от исходного питания схемы до интересующего i–го продукта. Двухмерный массив EPSCO(J, K) означает абсолютную сепарационную характеристику J-ой операции по концентрату, а кодировка EPSTA(J, K) означает то же самое по хвостам. Переходим к компьютерному кодированию вышерассмотренных теоретических формул для сепарационных характеристик. Частная сепарационная характеристика J-ой операции сепарации по концентрату EPSUN(J, K) есть отношение масс узкой K-фракции в концентрате и питании операции. Функция EPSUN(J, K) может быть представлена / аппроксимирована различными математическими формулами, например, экспоненциальный закон, гиперболический тангенс и др., что рассмотрено выше.  Кроме того, могут быть использованы N-ординатные числовые модели, например N = 10.  Например, частная сепарационная характеристика J-ой операции флотации по концентрату (обычная флотация, не колонная):

EPSUN(J,K) = 1 – exp ( - S(J) * T(J) * K),                                      (6.24)

где S(J) , T(J) - степень аэрации пульпы и время флотации в J-ой операции.

Абсолютная результирующая сепарационная характеристика полуканонической схемы в целом (с любым числом операций):

EPSres(K) = A / (A + B); EPSres(K) = EPSCO (1,K);                  

A = EPSUN(1,K)*EPSUN(2,K)*…*EPSUN(Ncl,K)*EPSUN(Ncl+1,K);

B = (1-EPSUN(Ncl+1,K))*(1-EPSUN(Ncl+2,K))*…*(1-EPSUN(Ncl+Nsc+1,K));    (6.25)

где: Ncl – число операций перечистной ветви (cleaner - перечистка), Nsc - число операций контродьной ветви (scavenger – контрольная операция).

Номинально операции схемы нумеруются, начиная от последней перечистки J = 1 через основную операцию  J= Ncl+1 до последней контрольной операции J= Ncl+Nsc+1.

Абсолютная результирующая сепарационная характеристика канонической схемы в целом (с любым числом операций):

EPSres(K) = A*G / (A*G + B*H); EPSres(K) = EPSCO (1,K);                        (6.26)

где:

A = EPSUN(1,K)*EPSUN(2,K)*…*EPSUN(Ncl,,K)*EPSUN(Ncl+1,K);

B = (1-EPSUN(Ncl+1,K))*(1-EPSUN(Ncl+2,K))*…*(1-EPSUN(Ncl+Nsc+1,K));

G = (1-EPSUN(Ncl+2,K))*(1-EPSUN(Ncl+3,K))*…*(1-EPSUN(Ncl+Nsc+1,K)) +

+ EPSUN(Ncl+2,K)*(1-EPSUN(Ncl+3,K))*…*(1-EPSUN(Ncl+Nsc+1,K)) +

+ EPSUN(Ncl+2,K)*EPSUN(Ncl+3,K)* …*(1-EPSUN(Ncl+Nsc+1,K)) +

+ EPSUN(Ncl+2,K)*EPSUN(Ncl+3,K)*…*EPSUN(Ncl+Nsc+1,K);

H = EPSUN(1,K)*EPSUN(2,K)* …*EPSUN(Ncl,K) +

+ (1-EPSUN(1,K))*EPSUN(2,K)*…*EPSUN(Ncl,K) +

+ (1-EPSUN(1,K))*(1-EPSUN(2,K))*…*EPSUN(Ncl,K) +

+ (1-EPSUN(1,K))*(1-EPSUN(2,K))*…*(1-EPSUN(Ncl,K))

Абсолютная сепарационная характеристика канонической схемы (с любым числом операций) от питания схемы до питания основной операции для J=Ncl+1:

EPSFE(Ncl+1,K) = G*H / (A*G + B*H);                                        (6.27)

где A, G, B, H – как выше.

Абсолютная сепарационная характеристика канонической схемы (с любым числом операций) от питания схемы до питания J-ой перечистной операции для J<Ncl+1:

EPSFE(J,K) = A*G*h / [ (A*G + B*H)*a]; J = 1, 2, 3, …, Ncl+1;                (6.28)

где: A, G, B, H – как выше,

; 

.

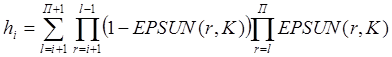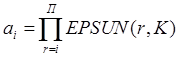Абсолютная сепарационная характеристика канонической схемы (с любым числом операций) от питания схемы до питания J-ой контрольной операции для J>Ncl+1:

EPSFE(J,K) = B*H*g / [ (A*G + B*H)*b]; J = Ncl+2, Ncl+3, …, Ncl+Nsc+1;      (6.29)

где: A, G, B, H – как выше,

; 

.

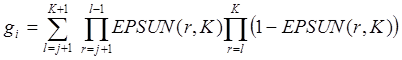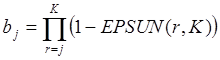Эти формулы показывают связь сепарационных характеристик с главными технологическими факторами.  Они используются в компьютерных программах для фракционного анализа (вычисление функций GAM, BET), а также  - для фракционно-балансных, прогнозирующих и оптимизирующих расчетов схем флотации.

Скачать файл