Взаимосвязь между извлечениями компонентов и сепарационными характеристиками схем. Методы и формулы для вычисления абсолютных сепарационных характеристики схем и их частей, страница 12

Так, для схем, представленных на рис.6.4,а, получается при и ; на рис.6.4,б – при и  (время флотации и степень аэрации операций всех схем соотнесено к простейшей схеме, представленной на рис. 6.1,а вместе с t и S).

Рассмотренный подход позволяет эквивалентировать схемы различной конфигурации. Заметим, что эквивалентности по сепарационной характеристике соответствует и эквивалентность схем по окончательным технологическим показателям – выходу концентрата: ; и содержанию компонента (металла) в концентрате: 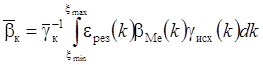 для одного и того же питания и . Для сравнения требуемого объема флотационных машин в схемах необходимы дополнительные расчеты.

Рассмотренный подход – эквивалентирование по и  – применим не только к флотационным схемам, но и к гравитационным, магнитным и другим схемам. См. Тихонов О.Н., Условия эквивалентности двух главных типов симметричных технологических схем. Изв.вузов, Горный журнал,   №3   1982, с.  116-118

6.7. Нахождение абсолютных сепарационных характеристик для схем любой конфигурации с помощью теории графов

Альтернативно приведенным выше в параграфе 6.1 методам нахождения абсолютных сепарационных характеристик (из частных) кратко рассмотрим еще один подход. Нахождение абсолютных сепарационных характеристик  для схем любой конфигурации (канонических или нет) возможно с использованием «правила циклов» Шеннона-Мэсона из теории линейных графов [См. Заде Р., Дезоер Ч., Теория линейных систем. М. Наука, 1970]. Ниже это поясняется применительно к обогатительным технологическим схемам.  Технологическая схема представляется в виде линейного ориентированного графа следующим образом, рис. 6.5.  Каждой операции (кружок на рис. 6.5, б) соответствует вершина графа, а каждому потоку минерального материала между парой связанных операций ставится в соответствие направленная дуга (стрелка), начинающаяся в i-й и заканчивающаяся в j-й вершине графа. Этой дуге приписывается коэффициент передачи, равный частной сепарационной характеристике операции по концентрату или хвостам (извлечению узкой фракции из i–го потока в j-й поток материала). Вершина источника (исходное питание схемы) связывается с входной вершиной графа дугой с единичным коэффициентом передачи (вершиной источника графа называется вершина, в которой не оканчивается ни одна дуга).

Правило Шеннона-Мэсона: Коэффициент передачи от входа к выходу в линейном графе (т.е. абсолютная сепарационная характеристика) определяется следующим ключевым выражением:

 = ,                                                  (6.24, а)

где:  - определитель графа; L_l  - коэффициент передачи l-го пути (путем называется незамкнутый ориентированный маршрут без повторяющихся дуг) между заданным входом и выходом, равным произведению коэффициентов передач всех дуг, образующих l-й путь; _l - определитель сокращенного графа, образующегося результате исключения из исходного графа l-го пути и всех дуг, имеющих с ним общие вершины.

Коэффициент передачи L_l представляет собой в рассматриваемой задаче сепарационную характеристику соответствующих участков схемы. Суммирование проводится по всем имеющимся путям, при этом путь по определению не содержит контуров (контур есть замкнутый ориентированный маршрут без повторяющихся вершин).

Определитель линейного графа может быть вычислен следующим образом:

,                                             (6.24, б)

где: - коэффициент передачи i-го контура и суммирование производится по всем контурам;  - является произведением коэффициентов передач j-й пары независимых контуров и суммирование производится по всем таким парам;  - является произведением коэффициентов передач k-й тройки независимых контуров и суммирование производится по всем таким тройкам и т.д. Контуры, проходящие через различную последовательность вершин, независимы, а если они проходят хотя бы через одну общую вершину, то они зависимы. Коэффициент передачи контура равен произведению коэффициентов передачи составляющих его дуг.