Взаимосвязь между извлечениями компонентов и сепарационными характеристиками схем. Методы и формулы для вычисления абсолютных сепарационных характеристики схем и их частей, страница 6

Последняя формула показывает, что крутизна характеристики схемы  возрастает в арифметической прогрессии с увеличением числа операций n. Если к основной операции добавить одну пару операций (перечистная и контрольная), то крутизна  для такой схемы (П = К =1) возрастает вдвое. Если добавить еще одну пару операций (перечистная и контрольная), то крутизна  для полученной схемы (П = К = 2) возрастает втрое и т. д. Доказательство основывается на формуле (6.10). Дифференцируя выражение  по ξ получаем производную от результирующей сепарационной характеристики схемы:

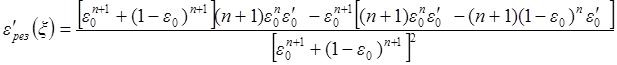. Подставляя с учетом , получаем формулу (6.15). Эта формула справедлива для гравитационных, магнитных, флотационных и других схем обогащения; с ее помощью по известной крутизне отдельной операции легко получить крутизну , для симметричной схемы в целом с любым П = К = n. Практически целесообразно пользоваться ею совместно с вычислением для типовых сепараторов. Например, для гравитационных схем с отсадочными машинами формула (6.15) принимает вид             . Для флотационных схем она принимает вид                        . Аналогичные формулы получаются для других схем. Простая формула (6.15) пригодна только для симметричных схем с идентичными операциями  и канонических.

Для несимметричных же схем и даже для симметричных при неидентичных операциях нужно исходить из формул (6.8) и (6.9), что усложняет анализ.

Для несимметричных канонических схем  имеет силу приближенная формула (П = n, К = m):

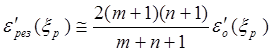.                                                                 (6.16, а)

Для несимметричных полуканонических схем  имеет силу приближенная формула (П = n, К = m):

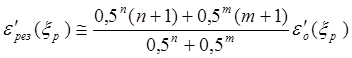.                                      (6.16, б)

Для несимметричных и канонических и полуканонических схем можно воспользоваться также следующей грубой оценкой:

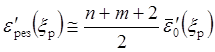,                                                                                (6.16, в)

где  - средняя крутизна частной сепарационной характеристики операции схемы.

При нахождении границы разделения  в тех же случаях  можно применить следующий упрощающий прием. В соответствии с формулой (6.8) величина результирующей сепарационной характеристики в точке  равна, рис. 6.2, а:

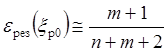.                                                                                            (6.16, г)

Здесь  - граница разделения для симметричной схемы n = m или, или для основной (любой) операции. Для симметричной схемы имеем n = m и получается  = 0,5. При преобладании перечистной ветви n > m граница разделения схемы смещается вправо, в сторону концентратных фракций; наоборот, при n < m граница смещается в сторону хвостовых фракций, рис. 6.2, а. Величина смещения может быть вычислена как катет примыкающего треугольника на рис. 6.2. С учетом этого треугольника формула для границы разделения несимметричной схемы получается в виде:

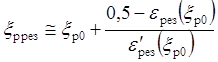.                                                                        (6.16, д)

С учетом  (6.16, а)  получается  для  несимметричных ‘сбалансированных’ () схем:

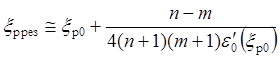.                                                            (6.16, е)    

Здесь  - крутизна частной сепарационной характеристики основной (любой) операции. Для симметричной схемы имеем n = m и получается .

В общем случае несимметричных и несбалансированных схем (и для нетиповых схем) по известной характеристике  находится  из уравнения   =0,5 , а также  находится  путем дифференцирования - компьютерными расчетами.

См. Тихонов О.Н., Анализ влияния числа перечистых и контрольных операций на точность флотационного обогащения. Труды ВНИИМеханобр, Математическое обеспечение АСУТП  1978  с. 108-111; Тихонов О.Н.,  Сепарационные характеристики незамкнутых флотационных схем с ячейками из трех операций. ИВУЗ-Горный журнал  №9    1979,  с. 118-121; Тихонов О.Н., Приближенное нахождение границы разделения и крутизны сепарационной характеристики несимметричных схем  обогащения. Изв.вузов, Горный журнал, №12, 1984, с.92-96;  Тихонов О.Н.,  Влияние числа перечистных и контрольных операций на крутизну сепарацион-ных характеристик схем обогащения углей. Труды 8-го Международного Конгресса по обогащению углей    т. 11 с.125-126  Донецк 1979.