Взаимосвязь между извлечениями компонентов и сепарационными характеристиками схем. Методы и формулы для вычисления абсолютных сепарационных характеристики схем и их частей, страница 13

Пример. Для иллюстрации применения описанной теории графов рассмотрим вычисление результирующей сепарационной характеристики схемы на рис. 6.5, а. Эта схема имеет разветвленную контрольную ветвь; содержит одну основную и четыре контрольных операции. Оборотные продукты возвращаются в предыдущие операции нетиповым образом (один из флотационных циклов Алмалыкской ОФ). Операции пронумерованы по часовой стрелке J = 1, 2, 3, 4. Частные сепарационные характеристики операций по их концентратам обозначены:. Частные сепарационные характеристики операций по их хвостам обозначены: .

Соответствующий рассматриваемой схеме граф на рис. 6.5, б имеет два независимых контура, коэффициенты передачи которых равны:

;   .

Откуда по формуле (6.24, б) получается определитель графа:

.

Имеются два пути от входа к выходу, поэтому:

L₁ = ;      ₁ = 1 – (1 -);   L₂ = (1 -);  ₂ = 1.

Следовательно, получаем результирующую сепарационную характеристику в виде:

.

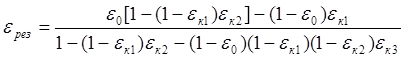Добавим пояснения. На рис. 6.5, б около стрелок написаны частные сепарационные характеристики операций по концентратам  и хвостам .  Кружки графа соответствуют операциям. Например, верхний (1-й) кружок соответствует основной операции (J = 1); в него направлены две стрелки: исходное питание и концентрат последней контрольной операции (J = 4); из него выходят две стрелки: концентрат и хвосты основной операции. Все эти стрелки ‘несут коэффициенты передачи’ в виде частных сепарационных характеристик операций. Сказанное относится и к другим операциям-кружкам и поясняет процедуру составления графа.

Рассмотренный подход с теорией графов целесообразно применять для нетиповых сложных схем, а для наиболее распространенных на практике типовых схем можно обойтись вышерассмотренными формулами (6.8, 6.11, 6.12). Применение теории графов является альтернативой универсальному методу с использованием потоков узких фракций q_i , рассмотренному в параграфе 6.1 (этот метод с q_i применим к любым схемам). См. Походзей Б.Б., Тихонов О.Н., Расчет и оптимизация схем флотационного обогащения с применением ЭВМ. 1983 г. Изд. ЛГИ, Л. 57 с.; Походзей Б.Б., Тихонов О.Н., Марковские модели процессов флотационного обогащения руд. Заводская лаборатория, 1987, №1, с. 40-48.]

Рис. 6.5. К примеру нахождения сепарационных характеристик с помощью графов.

6.8. Компьютерные расчеты сепарационных характеристик

Без компьютерной помощи теория разделения минералов не может использовать свой потенциал в полной степени. При пользовании компьютерными программами нужно иметь представление об их внутренней теоретической основе. Вначале рассмотрим формулы сепарационных характеристик, записанные для кодов распространенных компьютерных программ. Возможно читателю самому придется писать коды компьютерных программ для конкретных задач. Вышеприведенные формулы  для сепарационных характеристик и другие формулы теории (записанные греческими или русскими буквами) нужно писать латинскими буквами, желательно в наглядно объяснимой манере. Это необходимо при пользовании пакетами Microsoft Word, Microsoft Excel, которые имеют программирующий пакет VBA (Visual Basic for Applications); при более глубоком подходе используются текущие версии Visual Basic и / или Visual C++ . Специализированные ‘сепарационно-обогатительные’ компьютерные программы также вовлекаются в описываемые ниже компьютерные расчеты.

Скажем кратко о главных примерах кодовых обозначений. Частную сепарационную характеристику любой операции  можно записать в кодах программы в виде EPSUN(K), где EPS заменяет греческую букву , латинская буква K заменяет греческую букву , добавка UN соответствует английскому слову UNIT означающему ОПЕРАЦИЯ для технологических схем. Таким образом, делается кодировка → EPSUN(K). Если частная сепарационная характеристика операции относится к концентрату (англ. concentrate), то наглядна кодировка → EPSUNco(K) → EPSUN(K). Если частная сепарационная характеристика операции относится к хвостам операции (англ. tails), то наглядна кодировка → EPSUNta(K) → 1 - EPSUN(K), для двухпродуктовых операций.  В компьютерных программах фигурирует не одна, а несколько операций , составляющих технологическую схему; следовательно дополнительно вводится кодовый (идентификационный) номер-имя операции J, и двухмерный массив EPSUN(J, K) означает частную сепарационную характеристику по концентрату J-ой операции.