Взаимосвязь между извлечениями компонентов и сепарационными характеристиками схем. Методы и формулы для вычисления абсолютных сепарационных характеристики схем и их частей, страница 5

Абсолютных сепарационные характеристики участков схем  и  показывают извлечение любой фракции  в i-й (в частности, конечный) продукт от исходного питания. Подчеркнем роль абсолютных сепарационных характеристик участков схем, приведя базисные формулы для вычисления технологических показателей:

Выход (массовая доля) i-го продукта;

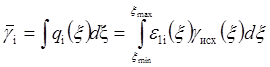;                                         (6.13 а)  

Содержание j-го компонента (%) в i-м продукте;

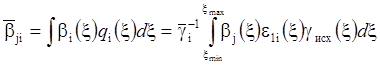,                      (6.13 б)

где:   – поток элементарной фракции в i-м продукте, т/час;  – абсолютная сепарационная характеристика участка схемы для i-го продукта (извлечение элементарной фракции от исходного в в i-й продукт);  j – номер ценного компонента.

Названные базисные формулы являются математически точными и применяются ниже для фракционно-балансных, прогнозирующих и оптимизирующих расчетов схем – с использованием фракционного состава сырья и сепарационных характеристик.

См.:  Tikhonov О. N.  Separational  Characteristics of Mineral Processing.—Mineral proc. Extractive Metallurgy Review,  1985, v. 2,  p. 105-134  (Gordon and  Breach S. P. Ltd., Gr. Britain); Назаров Ю.П., Тихонов О.Н., Моделирование промышленных флотационных схем. Изв.вузов, Горный журнал, №8, 1984, с. 47-49; Александрова Е.П., Елизаров Д.Б.,  Назаров Ю.П., Тихонов О.Н., Расчет на ЭВМ результирующих сепарационных характеристик флотационных и др. схем. В сб.”Совершен. методов переработки минерального сырья”, М., 1984, с. 146-151;  Елизаров Д.Б., Тихонов О.Н.,  Расчет на ЭВМ сепарационных характеристик схем обогащения. Изв.вузов, Горный журнал, 1984, №8,  с. 118-121.

6.3. Граница разделения и крутизна результирующей сепарационной характеристики в рабочей точке

Задачи анализа выясняют, как влияют конфигурация схемы, тип сепараторов в операциях, настроечные параметры сепараторов на абсолютные сепарационные характеристики  и . Характеристики  и  для конкретной схемы обогащения – гравитационной, магнитной, флотационной и других – получаются подстановкой частных сепарационных характеристик конкретных аппаратов (операций) , ,  схемы в рассмотренные выше общие формулы (6.8) - (6.10) для  и . Помимо вычисления абсолютных сепарационных характеристик анализ схем дополняется вычислением границ разделения схем и крутизны сепарационной характеристики  различных схем.

Положение границы разделения схемы и крутизна в рабочей точке  являются важнейшими параметрами результирующей сепарационной характеристики схемы . При этом схема рассматривается как одна операция – единым ‘блоком’. Величина является корнем уравнения: .

Аналитически это уравнение не всегда легко решается, особенно для сложных схем, поэтому на практике лучше пользоваться графическим методом: построить график ; на высоте  провести горизонталь до пересечения с графиком; опустить перпендикуляр в искомую точку . Или – применять компьютерные расчеты.

После нахождения  крутизну можно вычислить дифференцированием:                             .  Это всегда можно сделать по аналитической формуле для , либо графическим дифференцированием по тангенсу угла наклона касательной к  в рабочей точке . Графически можно найти крутизну  - как тангенс угла наклона касательной в рабочей точке  характеристики . В общем случае вычисление  и  не является простой задачей и желательно применение компьютерных расчетов. Представляет интерес нахождение аналитических формул для простых случаев.

Для симметричных канонических и полуканонических  схем  с идентичными операциями , имеет силу простая точная формула для границы разделения схемы:                     

,                                   (6.14)

т.е. граница разделения симметричных схем  совпадает с границей разделения основной (или любой) операции .  Для симметричных канонических и полуканонических схем имеет силу простая точная формула для крутизны результирующей сепарационной характеристики:

;                                                (6.15)

где – крутизна характеристики основной (и всех других) операций.