Взаимосвязь между извлечениями компонентов и сепарационными характеристиками схем. Методы и формулы для вычисления абсолютных сепарационных характеристики схем и их частей, страница 3

;

;

;

;

;

                            (6.7)

Результирующую сепарационную характеристику находят из третьей строки как отношение . Результирующая сепарационная характеристика является необходимой и достаточной для оценки и анализа схемы в целом как «большого» сепаратора с одним исходным питанием  и двумя конечными продуктами   и .

Абсолютные сепарационные характеристики для промежуточных продуктов (участков) схем имеют также важное значение; спецификой оборотных продуктов является наличие максимумов в окрестности границы разделения схемы. Сепарационная характеристика  для любого i-го продукта (по отношению к исходному питанию) равна отношению производительностей (масс) по фракции  в данном продукте и в питании схемы, т.е. . Для всех продуктов схемы она находится решением упомянутых линейных алгебраических уравнений аналогично ; она является частным случаем, когда . Для рассматриваемого примера (см. рис.6.1,г)  все эти внутренние характеристики приведены в формулах (6.7) в виде . Практически важной является только половина набора характеристик, (например, для частных концентратов всех операций), остальные характеристики легко находят по формуле (6.5).

Таким образом, первоначальное описание схемы с помощью  частных характеристик  операций превращается в описание, состоящее из такого же числа абсолютных сепарационных характеристик  для концентратов отдельных операций. Из этих  характеристик  важнейшей является результирующая характеристика . Например, для схемы, приведенной на рис.6.1,г, вместо  и вводятся ,   и  .

Заметим, что иногда при анализе отдельных участков сложных схем могут представлять интерес «перекрестные» сепарационные характеристики от j-го промпродукта до i-гo промпродукта. Например, для схемы, приведенной на рис. 6.1, г, от концентрата  контрольной операции до окончательного концентрата  получается .

Каноническая и полуканоническая схемы с любым числом операцийважны для анализа из-за их распространенности. Действуя по рассмотренной выше методике для общего случая канонической схемы с любым числом перечистных П и контрольных К операций можно получить результирующую сепарационную характеристику в виде:

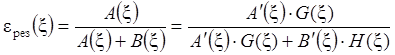;                                 (6.8)

где: ; ;

; ;

.

Здесь , ,  – сепарационные характеристики соответственно основной, перечистных и контрольных операций. Приведем пояснения к формуле (6.8) для пользования и запоминания. Количество  есть произведение сепарационных характеристик по концентрату всех операций перечистной ветви вместе с основной операцией. Количество  есть произведение сепарационных характеристик всех операций по хвостам контрольной ветви вместе с основной операцией. Количество  есть сумма, в которой первый член равен произведению сепарационных характеристик по хвостам всех операций контрольной ветви; в каждом последующем члене один бином  заменяется на «моном» ; последний член равен . Количество  есть сумма, в которой первый член равен произведению сепарационных характеристик по концентрату всех операций перечистной ветви; в каждом последующем члене один «моном»  заменяется на один бином

(1-); последний член равен .

Для полуканонической схемы (рис. 6.1, е), в которой все оборотные продукты возвращаются в голову основной операции, результирующая характеристика имеет вид:

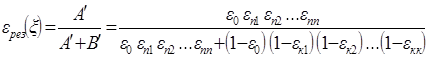                         (6.9)

Здесь  и  – такие же как в формуле (6.8). Формулы (6.8), (6.9) получаются теми же методами, т. е. решением системы линейных алгебраических уравнений баланса по узкой фракции . Формулы (6.8), (6.9) являются математически точными.

Важным является также частный случай симметричной схемы (с одинаковым числом перечистных и контрольных операции П = К = п с дополнительным условием взаимной идентичности всех частных сепарационных характеристик: . Такие симметричные схемы с идентичными операциями (и канонические, и полуканонические), имеют простое выражение для результирующей характеристики:

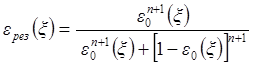                                             (6.10)