Для электромагнитных колебаний в идеальном колебательном контуре (контур состоит только из ёмкости С и индуктивности L) заряд q на одной из пластин конденсатора также изменяется по закону синуса или косинуса:
(5.3)
или
(5.4)
где q0 − амплитудное значение заряда на одной из пластин конденсатора.
Для механических колебаний:
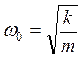(5.5)
где k – коэффициент пропорциональности,
m – масса колеблющегося тела.
Для электромагнитных колебаний
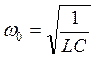(5.6).
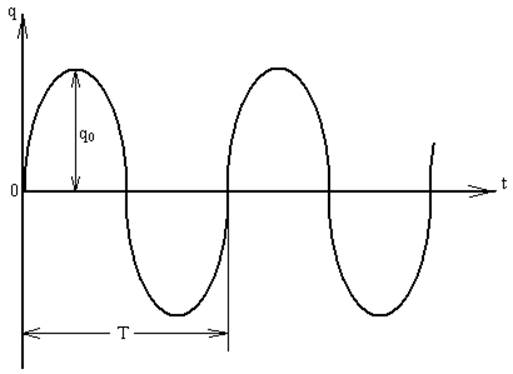
Графики зависимостей x(t), q(t) соответствуют незатухающим гармоническим колебаниям, Рисунок 21, 22.
Рисунок 21
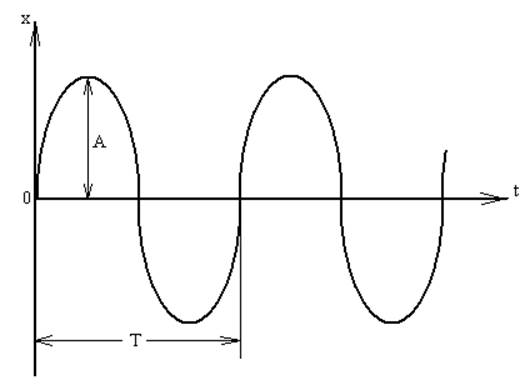
Рисунок 22
Периоды Т механических и электромагнитных колебаний (то есть время одного полного колебания), соответственно равны для механических колебаний:
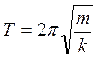(5.7)
для пружинного маятника
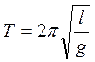(5.8)
для математического маятника, где
−
ускорение свободного падения.
k – жёсткость пружины
m – масса груза, подвешенного к пружине
l – длина нити подвеса в математическом маятнике.
Для электромагнитных колебаний
(5.9)
Следовательно, периоды свободных (собственных) механических и электромагнитных колебаний определяются параметрами колеблющихся систем, а сами колебания – являются незатухающими
5.2 Затухающие колебания.
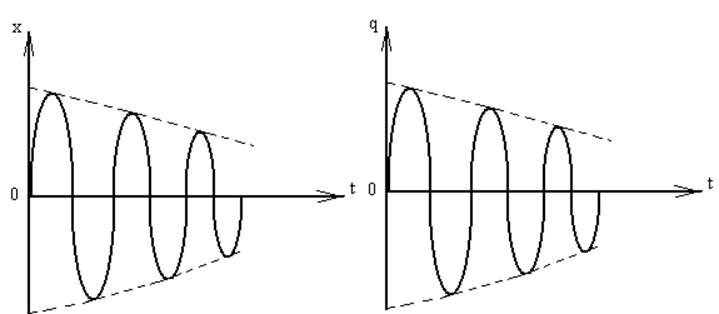
Причиной затуханий механических колебаний является наличие сил сопротивления в реальной среде, так как часть энергии в процессе колебания затрачивается на преодоление сопротивления и в результате полная энергия колеблющегося тела уменьшается, а само механическое колебания затухает. Причиной затухания электромагнитных колебаний в реальном колебательном контуре, Рисунок 21, является наличие сопротивления R и соответственно, потери энергии на выделение тепла на сопротивлении.
Для механических затухающих колебаний:
β − коэффициент затухания.
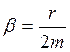(5.10)
где r – коэффициент сопротивления среды
m – масса колеблющегося тела.
Уравнение затухающих колебаний имеет вид:
(5.11)
или
(5.12)
где А0 – начальная амплитуда колебания
ω – круговая или циклическая частота затухающих колебаний
φ0 – начальная фаза колебаний.
Связь ω,ω0, β имеет вид:
(5.13)
или с учётом (5.11, 5.12)
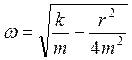(5.14).
Для электромагнитных затухающих колебаний: уравнение колебаний:
(5.15)
или
(5.16)
где q0 – начальное амплитудное значение заряда на одной из пластин конденсатора.
Для затухающих электромагнитных колебаний
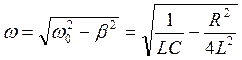(5.17).
Графики затухающих механических и электромагнитных колебаний представлены на рис. 23, 24.
Рис. 23 Рис. 24
Периоды затухающих колебаний определяются:
для механических колебаний с учётом (5.14)
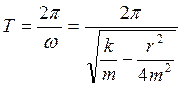(5.18)
для электромагнитных колебаний с учётом (5.17)
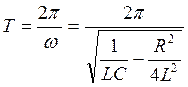(5.19).
Из (142, 143) следует, что периоды затухающих механических и электромагнитных колебаний определяются параметрами системы.
В реальных системах колебания не возникнут в случае:
критического сопротивления среды, rкр, для механических колебаний:
(5.20)
критического сопротивления Rкр в колебательном контуре:
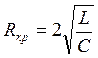(5.21).
Важными характеристиками затухания колебаний (механических, электромагнитных) являются:
λ – логарифмический декремент затухания
Θ – добротность системы
(5.22)
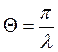(5.23).
Следовательно, добротность колеблющейся системы (5.23) тем выше, чем меньше логарифмический коэффициент λ затухания.
Сравнение приведённых формул и графиков для затухающих механических и электромагнитных колебаний позволяет установить общие закономерности в процессах обоих видов колебаний.
5.3 Вынужденные колебания.
Для осуществления вынужденных механических и электромагнитных колебаний необходимо периодически восполнять потери энергии, как механической системы, так и реального колебательного контура.
Для механической системы убыль энергии восполняется за счёт периодически действующей силы F:
(5.24)
где F0 – амплитудное значение силы F,
ω – круговая (или циклическая) частота вынужденных колебаний.
Для электромагнитных колебаний убыль энергии восполняется за счёт периодически действующей эдс в цепи реального колебательного контура:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.