Законы механики Ньютона. Понятие замкнутой системы. Электростатика. Электрический ток. Электромагнетизм. Понятие магнитного потока. Индукция, страница 2

Для абсолютно упругого удара характерно, что после удара тела полностью восстанавливают свою форму. Тела после удара движутся отдельно друг от друга со скоростями  и . На рисунке представлены два шара массами m₁ и  m₂  до и после удара. До удара скорости тел  и

                        

Рисунок 3 (До удара)         Рисунок 4 (После удара)

В соответствии с законом сохранения импульса имеем:

      (1.10).

1.3. Законы сохранения энергии. Виды энергий.

Энергия любой системы тел или тела характеризует способность системы тел или тела совершать работу.

Энергия любой системы равна сумме различных видов энергии: кинетической, потенциальной, тепловой и т.д.

Для тела массой m, имеющего скорость , кинетическая энергия равна

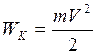  (1.11)

Потенциальная энергия – это энергия взаимодействующих тел. Для тела массой m потенциальная энергия его взаимодействия с Землёй равна

 (1.12)

h – высота, на которой находится тело от поверхности Земли, с которой связан нулевой уровень отсчёта потенциальной энергии.

Потенциальная энергия упруго деформированной пружины определяется через: величину деформации x и коэффициент k жёсткости по формуле

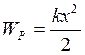      (1.13)

Полная энергия тела складывается из кинетической и потенциальной энергии:

(1.14)

Если система замкнутая, то закон сохранения энергии утверждает, что полная энергия замкнутой системы остаётся постоянной, то есть не изменяется со временем. Для незамкнутой системы закон сохранения энергии формулируется в виде: энергия не исчезает бесследно, и не появляется вновь, она лишь превращается из одного вида в другой.

Электростатика.

2.1. Взаимодействие точечных зарядов. Закон Кулона. Физический смысл напряжённости электрического поля.

Используя опыты с крутильными весами, Кулон в 1785 году вывел закон взаимодействия двух точечных зарядов  и , находящихся на расстоянии r друг от друга. Точечными называются такие заряженные тела, размерами которых можно пренебречь по сравнению с расстоянием между ними. По закону Кулона сила F взаимодействия зарядов равна:

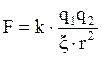   (2.1)

где ξ – относительная диэлектрическая проницаемость среды, k – коэффициент пропорциональности, равный в системе СИ:

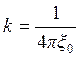      (2.2)

где 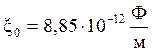 – диэлектрическая постоянная.

С учётом , .

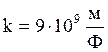Взаимодействие между зарядами осуществляется через электростатическое поле. К числу основных характеристик электростатического поля относится физическая векторная величина  – напряжённость, численно равная силе

, действующей на единицу положительного заряда, помещённого в данную точку поля.

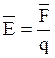(2.2).

Напряжённость электростатического поля, созданного точечным зарядом q на расстоянии r от заряда равна:

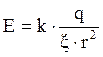   (2.3).

С вектором напряжённости  связана ещё одна характеристика электростатического поля, вектор , вектор электростатической индукции (или электростатического смещения).

      (2.4).

Графически электростатические поля принято изображать силовыми линиями напряжённости . Линии проводят так, что касательные к линиям совпадают с направлением вектора  в данной точке поля.

Если поле создано системой зарядов: , то для вектора результирующей напряжённости выполняется принцип суперпозиции: результирующая напряжённость в каждой точке поля равна геометрической сумме напряжённостей полей: , созданных в этой точке отдельными зарядами:

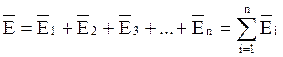  (2.5).

Аналогично, для вектора электрического смещения:

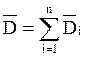     (2.6).

2.2. Поток вектора напряжённости. Теорема Остроградского-Гаусса и её применение.

Методы расчетов напряжённости  электростатических полей, созданных заряженными телами, основаны на применении принципа суперпозиции полей и теоремы Остроградского-Гаусса.

Теорема Остроградского-Гаусса определяет поток вектора  через произвольную замкнутую поверхность S, заключающую в себе электрические заряды:

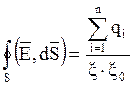       (2.5)

где ξ – относительная диэлектрическая проницаемость среды, ξ₀ – диэлектрическая постоянная.

В формуле (2.5) 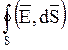 выражает математически поток вектора напряжённости  через замкнутую поверхность S, который характеризует общее число силовых линий вектора , пронизывающих замкнутую поверхность S.