Выразим r, dl из 
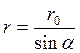(4.31)
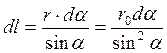(4.32)
Где учтено, что
(4.33).
По принципу суперпозиции магнитных полей и с учётом закона Био-Савара-Лапласа (4.27) получим выражение индукции В магнитного поля, созданного током в прямом проводнике конечной длины (с учётом (4.31-4.33)):
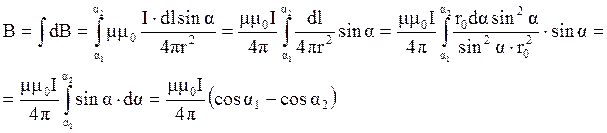(4.34)
Следовательно, индукция В и напряжённость Н магнитного поля, созданного током I в прямом проводнике конечной длины, определяются, как:
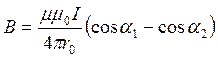(4.35)
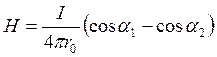(4.36).
Если прямой проводник
бесконечной длины, то 
Тогда из (112, 113) следует:
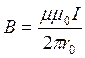(4.37)
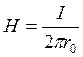(4.38), так как 
.
В системе СИ индукция
В магнитного поля измеряется в теслах [Тл], а напряжённость Н магнитного поля
измеряется в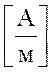 
.
4.5 Понятие магнитного потока. Индукция, самоиндукция.
Магнитный поток Ф – это физическая скалярная величина, численно равная числу силовых линий индукции магнитного поля, пронизывающих поверхность площадью S, рис. 18
Рисунок 18
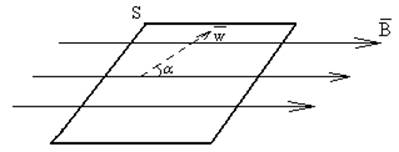На рис. 18 показана
плоская поверхность S,
−
нормаль к плоскости
α – угол между и
направлением силовой линии индукции 
магнитного
поля.
Для плоской поверхности магнитный поток
(4.39).
Если поверхность S имеет произвольную форму, то:
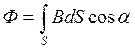(4.40).
Единицей измерения магнитного потока в системе СИ является вебер [Вб].
При перемещении проводника с током I или контура с током I в магнитном поле индукцией В совершается работа
(4.41)
где
−
изменение магнитного потока, связанное с перемещением проводника или контура во
внешнем магнитном поле.
В 1831г. Фарадей экспериментально открыл явление электромагнитной индукции, которое заключается в том, что:
во всяком замкнутом проводящем контуре при изменении магнитного потока через площадь, ограниченную этим контуром, возникает электрический ток, называемый индукционным.
Величина эдс индукции
по закону Фарадея определяется скоростью изменения магнитного потока, 
,
через поверхность проводящего контура.
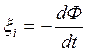(4.42).
Знак (-) в (4.42) выражает правило Ленца:
индукционный ток в контуре всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.
Для контура с М витками, полный магнитный поток:
(4.43)
а следовательно эдс индукции,
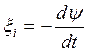(4.44).
Явление
электромагнитной индукции широко используется в работе генераторов и
электродвигателей. Не меньший практический интерес имеет явление самоиндукции:
при изменении силы тока в замкнутом контуре в нём индуцируется эдс самоиндукции
:
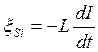(4.45)
где L – индуктивность контура,
−
быстрота изменения тока в контуре.
Знак (-) обусловлен правилом Ленца:
наводимый в контуре индукционный ток препятствует всякому изменению тока в контуре.
Для соленоида с числом витков N, площадью поперечного сечения S, длиной l по оси, индуктивность равна:
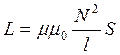(4.46)
где μ – относительная магнитная проницаемость материала сердечника
μ0 – магнитная постоянная.
Для ферромагнетика μ>>>1, и следовательно при введении в соленоид ферромагнитного сердечника, индуктивность соленоида значительно возрастёт. Для диамагнетика μ<1, и следовательно, введение сердечника из диамагнетика внутрь соленоида, индуктивность в соленоиде уменьшится. Энергия магнитного поля соленоида
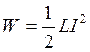(4.47).
5. Колебания (механические и электромагнитные).
Свободные (или собственные) колебания.
Рисунок 19. Рис. 20 Рис. 21
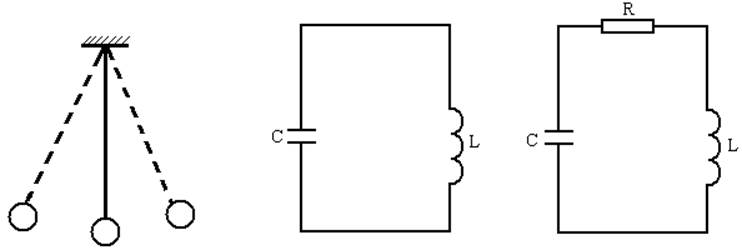
Рассмотрим механическую систему, например математический маятник, рис. 19, выведенную из положения равновесия и в дальнейшем, предоставленную самой себе. В отсутствие сопротивления внешней среды колебания такой системы являются свободными (или собственными) и продолжаются бесконечно долго. Уравнение колебания имеет вид:
(5.1)
или
(5.2)
где x – смещение колеблющегося тела от положения равновесия,
А – амплитуда колебания, А=хмах
− круговая или циклическая частота
собственных колебаний
t – время
φ0 – начальная фаза
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.