Законы механики Ньютона. Понятие замкнутой системы. Электростатика. Электрический ток. Электромагнетизм. Понятие магнитного потока. Индукция, страница 6

Рисунок 9.

Общее значение ξ равно:

 (3.23)

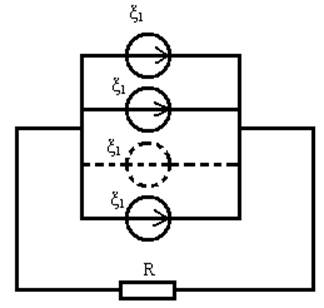
Общее значение внутреннего сопротивления

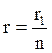 (3.24).

Ток I во внешней цепи по закону Ома для полной цепи (3.5) равен:

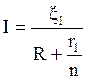 (3.25)

В реальных схемах может быть представлено смешанное соединение источников тока. Тогда надо учитывать соответствующие закономерности для последовательного и параллельного соединения как источников тока, так и резисторов.

4. Электромагнетизм.

4.1 Действие магнитного поля на проводник с током. Физический смысл индукции магнитного поля.

Если прямолинейный проводник длиной l по которому идёт ток I, помещён в магнитное поле, то на него со стороны магнитного поля действует сила F_A, равная по закону Ампера

 (4.1)

где B – индукция магнитного поля

α – угол между направлениями тока в проводнике и индукции магнитного поля.

Направление силы Ампера определяется правилом левой руки: ладонь левой руки надо расположить так, чтобы четыре пальца были направлены по направлению тока в проводнике; индукция магнитного поля должна входить в ладонь. Тогда отогнутый большой палец покажет направление силы Ампера.

Из (1) следует, что максимальное значение силы Ампера:

 (4.2)

при sinα=1 (α=90⁰).

Из (2)

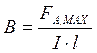 (4.3).

Из (3) следует физический смысл индукции: индукцией магнитного поля называется физическая векторная величина, численно равная максимальному значению силы Ампера, действующей на единицу длины прямолинейного проводника, по которому идёт единица силы тока.

Направление вектора индукции совпадает с направлением силы Ампера.

Индукция В магнитного поля измеряется в теслах [Тл].

4.2 Действие магнитного поля на движущийся заряд.

На заряд, движущийся в магнитном поле, действует сила Лоренца, F_Л.

Сила Лоренца определяется величиной заряда, q; скоростью заряда V, индукцией В магнитного поля:

 (4.4)

где α – угол между направлениями , .

Если на заряд одновременно действуют электрическое поле, напряжённостью , и магнитное поле, то на заряженную частицу действует результирующая сила

 (4.5).

Направление силы Лоренца для положительного заряда находится по правилу левой руки, (рис. 10)

Рисунок 10.                                         Рисунок 11.

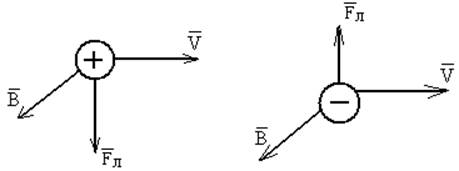
В зависимости от значения угла α могут быть рассмотрены различные случаи движения заряженной частицы.

Случай 1.

Частица влетает со скоростью  в магнитное поле вдоль силовой линии индукции магнитного поля. Следовательно α=0, sin0=0, F_Л=0.

Вывод: влетев в поле, частица продолжит своё движение вдоль силовой линии индукции равномерно и прямолинейно, так как сила Лоренца на частицу не действует.

Случай 2.

Заряженная частица влетает в магнитное поле со скоростью , перпендикулярной индукции магнитного поля , то есть α=90⁰.

Тогда из (4.4) получим:

 (4.6).

В этом случае сила Лоренца создаёт центростремительное ускорение, а сама сила Лоренца будет играть роль центростремительной силы F_ЦС, причём:

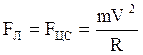 (4.7)

где R – радиус окружности, по которой заряженная частица будет двигаться в магнитном поле, m – масса частицы.

Из (4.6, 4.7) следует:

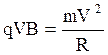 (4.8)

откуда

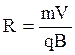 (4.9).

Следовательно радиус окружности R определяется удельным зарядом 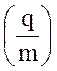 частицы, скоростью V частицы и значением индукции В магнитного поля.

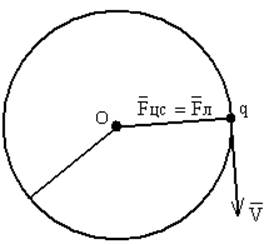
На рис. 12 показано движения заряженной частицы по окружности с центром в точке О.

Рисунок 12.

Период (то есть время одного полного оборота) Т определяется, как:

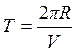 (4.10)

Из (4.9, 4.10) следует:

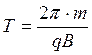 (4.11).

Следовательно, период Т обращения заряженной частицы по окружности зависит только от удельного заряда частицы и значения индукции магнитного поля, но не зависит от скорости частицы.

Случай 3.

Заряженная частица влетает в магнитное поле со скоростью , направленной под произвольным углом к направлению индукции магнитного поля (причём случаи 1,2 исключаются).

Рис. 13

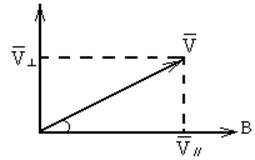
На рис. 13 показаны проекции скорости  и , причём:

 совпадает с направлением индукции

 перпендикулярна .

 (4.12)

 (4.13).

Движение заряженной частицы можно представить, как результат двух движений: