где μ=1 (для воздуха, так как сердечник отсутствует);
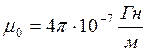
Из (3, 4) объёмная плотность энергии магнитного поля соленоида равна:
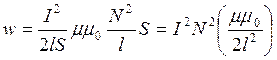 (5)
(5)
Из (5)
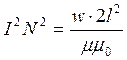 (6)
(6)
откуда число ампер-витков равно:
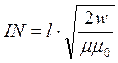 (7).
(7).
Вычислим по (7)
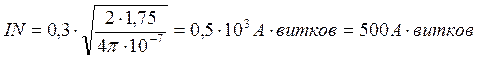
Ответ: ![]()
Задача №11.
Электрон (![]() ,
,
![]() ),
ускоренный разностью потенциалов
),
ускоренный разностью потенциалов ![]() ,
влетел в однородное магнитное поле с индукцией
,
влетел в однородное магнитное поле с индукцией ![]() и
стал двигаться по окружности.
и
стал двигаться по окружности.
Определить: радиус окружности и период обращения электрона по окружности.
|
Дано:
|
Рис.
|
|
R-? T-? |
На Рисунок показана
окружность радиуса R, по которой движется электрон е со скоростью ![]() ;
сила Лоренца
;
сила Лоренца ![]() ,
действующая на электрон, равна центростремительной силе
,
действующая на электрон, равна центростремительной силе ![]() и
направлена к центру окружности.
и
направлена к центру окружности.
![]() (1)
(1)
Учтём, что
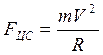 (2)
(2)
![]() (3)
(3)
где е – заряд электрона, m – масса электрона, В – индукция магнитного поля.
Из (1, 2, 3)
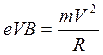 (4)
(4)
откуда
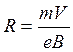 (5)
(5)
Период обращения по окружности равен времени, за которое электрон совершит один полный оборот по окружности.
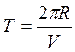 (6)
(6)
Для расчётов R, T определим скорость V электрона, влетевшего в магнитное поле, зная величину ускоряющей разности потенциалов U.
Учтём при этом, что
кинетическая энергия электрона (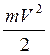 )
равна работе сил электрического поля, то есть
)
равна работе сил электрического поля, то есть
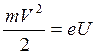 (7)
(7)
откуда
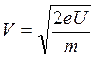 (8)
(8)
Вычисления:
по (8) 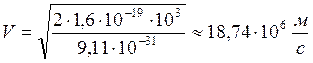
по (5) 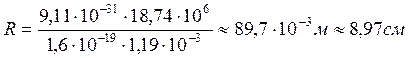
по (6) 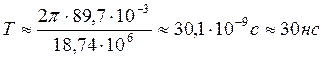
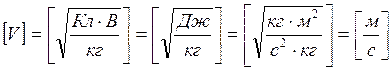
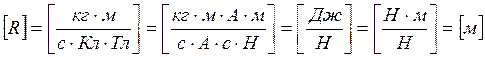
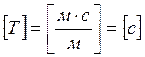
Ответ: ![]()
![]()
Задача 12.
Уравнение колебания
точки задано уравнением 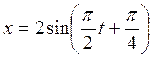 ,
см. Определить основные характеристики колебаний, максимальные значения
скорости и ускорения точки.
,
см. Определить основные характеристики колебаний, максимальные значения
скорости и ускорения точки.
|
Дано:
|
Основными характеристиками колебания являются А – амплитуда, ω0 – круговая или циклическая частота собственных колебаний.
Т – период( время одного полного колебания; f – линейная частота колебаний (число колебаний за 1 с.) |
|
Основные характеристики ?
|
Из вида данного уравнения:
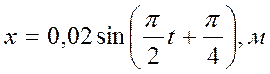 ;
при сопоставлении с общим видом уравнения
;
при сопоставлении с общим видом уравнения
![]() ,
получим: А=0,02м;
,
получим: А=0,02м; 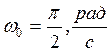 ;
;
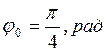 ;
;
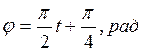 .
.
Учтём, что:
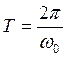 (1)
(1)
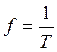 (2)
(2)
Тогда: 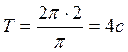 ;
;
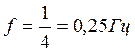
Скорость V и ускорение а колеблющейся точки определим через производные:
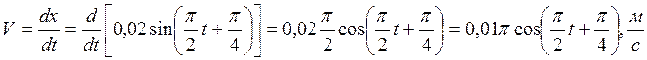 (3)
(3)
Из (3) максимальная скорость равна:
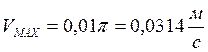 (4)
(4)
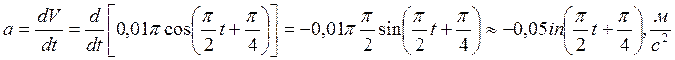 (5)
(5)
Из (5) максимальное ускорение равно:
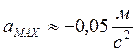
Ответ: А=0,02м; 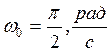 ;
;
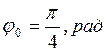 ;
;
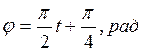 ;
;
![]() ;
;
![]() ;
;
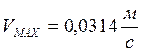 ;
;
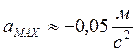 .
.
Задача №13.
Какое сопротивление R надо
ввести в (L-C) контур; ![]() ,
,
![]() ;
чтобы изменить частоту колебаний на 0,1%. Увеличится или уменьшится частота
колебаний.
;
чтобы изменить частоту колебаний на 0,1%. Увеличится или уменьшится частота
колебаний.
|
Дано:
|
Рисунок 1 Рисунок 2
|
|
R-? |
До введения в контур сопротивления R, контур является идеальным, (Рисунок 1). После введения сопротивления R контур стал реальным, (Рисунок 2).
Запишем формулу частоты
![]() электромагнитных
колебаний для каждого случая. Для этого используем:
электромагнитных
колебаний для каждого случая. Для этого используем:
формулы периодов колебания, связь линейной частоты с периодом а) для Рисунок 1.
![]() (1)
(1)
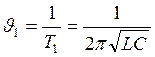 (2)
(2)
б) для рис. 2.
 (3)
(3)
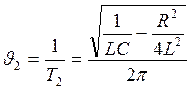 (4)
(4)
Сопоставим (2, 4)
откуда следует, что с введением сопротивления частота ![]() электромагнитных
колебаний уменьшится, то есть
электромагнитных
колебаний уменьшится, то есть
![]() (5)
(5)
Подставим в (5) уравнения (2, 4)
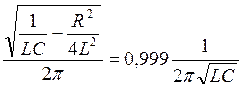 (6)
(6)
и возведём (6) в квадрат:
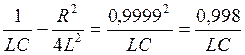 (7).
(7).
Из (7) 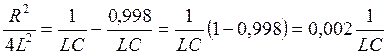 или
или
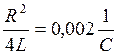 (8)
(8)
откуда:
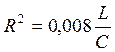 (9)
(9)
или
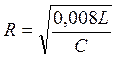 (10)
(10)
Вычислим значение
сопротивления по (10) 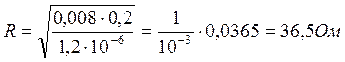
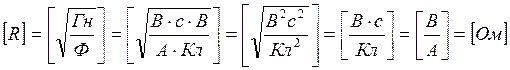
Ответ: ![]()
III Цикл лабораторных работ по физике ч I.
Лабораторная работа №1
Определение ёмкости конденсатора методом периодической зарядки, разрядки.
Цель работы: определить ёмкость каждого из двух конденсаторов, ёмкость при их последовательном и параллельном соединениях методом периодической зарядки и разрядки.
Приборы: амперметр, вольтметр, реостат, исследуемые конденсаторы, сеть переменного тока, автоматический переключатель.
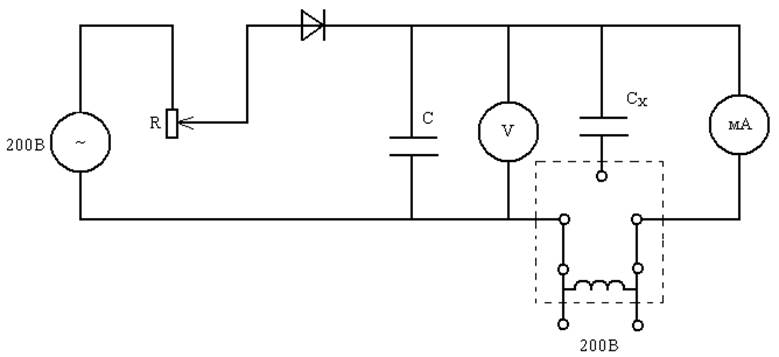
При периодической зарядке конденсатора от источника напряжения и его разрядке через миллиамперметр, будет измеряться средняя сила тока, если период собственных колебаний подвижной системы миллиамперметра во много раз больше времени разряда конденсатора.
Ёмкость СХ исследуемого конденсатора выражается через силу тока I в цепи, напряжение на конденсаторе, U и частоту f переменного тока сети.
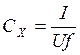 .
.
Порядок выполнения работы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.