1) равномерного
прямолинейного вдоль индукции ![]() со
скоростью
со
скоростью ![]() .
.
2) равномерного
движения по окружности со скоростью ![]() в
плоскости, перпендикулярной индукции
в
плоскости, перпендикулярной индукции ![]() магнитного
поля.
магнитного
поля.
В итоге заряженная частица будет двигаться по винтовой линии радиусом R и шагом h, рис. 14
Рис. 13
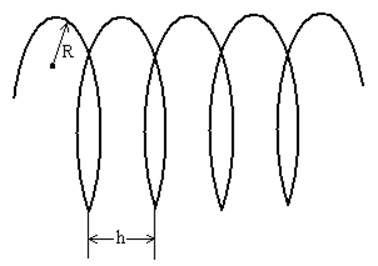
Шаг и радиус винтовой линии определяются, как:
![]() (4.14)
(4.14)
где Т – период, т.е. время одного оборота по витку винтовой линии.
Из (4.14, 4.11, 4.12) следует, что:
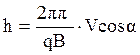 (4.15)
(4.15)
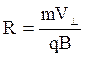 (4.16)
(4.16)
Из (90, 93) следует, что:
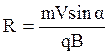 (4.17).
(4.17).
Таким образом, в неоднородном магнитном поле значения шага h и радиуса R винтовой линии уменьшаются с увеличением индукции В магнитном поле, на этом свойстве основана фокусировка заряженных частиц в магнитном поле.
4.3. Действие магнитного поля на рамку с током.
В качестве рамки с током рассмотрим прямоугольный контур ACDE со сторонами AC=DE=a; CD=AE=b.
Контур находится в
однородном магнитном поле, причём силовые линии индукции магнитного поля ![]() лежат
в плоскости рамки, рис. 14
лежат
в плоскости рамки, рис. 14
Рисунок 14
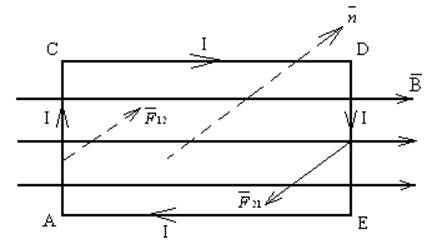 Пусть ток I в
рамке идёт по часовой стрелке.
Пусть ток I в
рамке идёт по часовой стрелке.
![]() –
нормаль к плоскости рамки.
–
нормаль к плоскости рамки.
Сила Ампера действует
лишь на стороны рамки: AC, DE, так как для сторон CD, EE угол
α между направлением тока и направлением индукции
равен соответственно ![]() .
.
Обозначим силы
Ампера, действующие на стороны AC, DE соответственно ![]() .
Направление сил
.
Направление сил ![]() показаны
на Рисунок в соответствии с направлением левой руки.
показаны
на Рисунок в соответствии с направлением левой руки.
![]() (4.18)
(4.18)
![]() (4.19).
(4.19).
Так как направления сил противоположны, а по величине эти силы равны, то создаваемый ими вращательный момент М, равен:
![]() (4.20)
(4.20)
или с учётом (4.18)
![]() (4.21)
(4.21)
где
![]() –
площадь рамки.
–
площадь рамки.
Обозначим
![]() (4.22)
(4.22)
как магнитный момент контура.
Тогда максимальный
вращательный момент, созданный парой сил ![]() равен:
равен:
![]() (4.23).
(4.23).
Указанный
вращательный момент повернёт плоскость контура в положение, в котором плоскость
контура будет перпендикулярна силовым линиям индукции ![]() магнитного
поля.
магнитного
поля.
Если же угол α между
нормалью ![]() к
плоскости контура и направлением индукции
к
плоскости контура и направлением индукции ![]() произволен,
то вращательный момент М равен:
произволен,
то вращательный момент М равен:
![]() (4.24)
(4.24)
или
![]() (4.25)
(4.25)
Рассмотренное выше действие магнитного поля на контур с током широко используется в измерительных приборах (амперметрах, вольтметрах) магнитоэлектрической системы, а также в устройстве и принципе действия электродвигателя постоянного тока.
4.4 Закон Био-Савара-Лапласа и примеры его применения к расчёту магнитных полей.
В 1820 году Био и
Савар экспериментально исследовали магнитные поля, создаваемые токами в проводниках
различной формы. Лаплас, анализируя результаты экспериментов, пришёл к выводу
расчёта индукции ![]() ,
создаваемой элементом тока
,
создаваемой элементом тока ![]() в
точке А, рис. 15
в
точке А, рис. 15
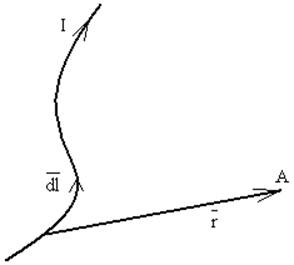
Рисунок 15.
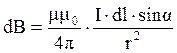 (4.26)
(4.26)
где ![]()
![]() –
магнитная постоянная.
–
магнитная постоянная.
μ – относительная магнитная проницаемость среды.
I – сила тока в проводнике.
r – длина радиуса-вектора ![]() .
.
α – угол между
элементом тока ![]() и
направлением
и
направлением ![]() -вектора.
-вектора.
Так как напряжённость
![]() магнитного
поля связана с индукцией
магнитного
поля связана с индукцией ![]() :
:
![]() (4.27)
(4.27)
то напряжённость магнитного поля dH, созданного элементом тока dl определяется, как:
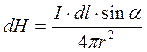 (4.28)
(4.28)
Формулы (4.26, 4.28) выражают закон Био-Савара-Лапласа, который используется для расчётов индукции и напряжённости магнитного поля, созданного током в проводниках различной формы.
В качестве первого примера рассмотрим круговой контур радиуса R, по которому идёт ток I, Рисунок 16.
Рисунок 16.
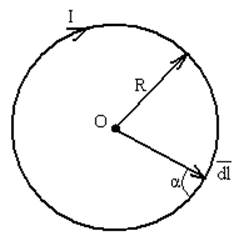 Разобьём контур на
малые элементы и выделим один из них,
Разобьём контур на
малые элементы и выделим один из них, ![]() .
Для любого элемента угол
.
Для любого элемента угол ![]() ,
а индукция
,
а индукция ![]() в
точке О по правилу буравчика направлена от нас перпендикулярно плоскости
контура. Следовательно, используя принцип суперпозиции магнитных полей, получим
с использованием (4.27)
в
точке О по правилу буравчика направлена от нас перпендикулярно плоскости
контура. Следовательно, используя принцип суперпозиции магнитных полей, получим
с использованием (4.27)
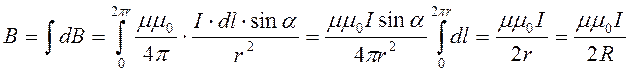 (4.29)
(4.29)
где учтено, что r=R.
Соответственно,
напряжённость магнитного поля: 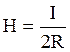 (4.30).
(4.30).
В качестве второго примера рассмотрим прямой проводник с током I, конечной длины, Рисунок 17.
Рисунок 17.
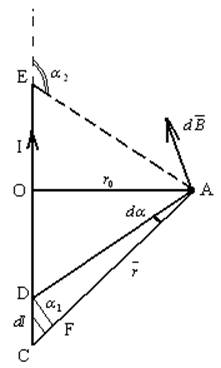 Обозначим:
Обозначим:
CE – длина проводника
OA=r0 – расстояние от точки А (в которой вычисляется индукция магнитного поля) до проводника.
α1, α2
– углы между направлением тока в проводнике и направлением радиуса-вектора ![]() на
нижний и верхний концы провода.
на
нижний и верхний концы провода.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.