Законы механики Ньютона. Понятие замкнутой системы. Электростатика. Электрический ток. Электромагнетизм. Понятие магнитного потока. Индукция, страница 4

Введём обозначения:

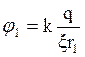      (2.21)

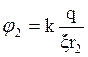     (2.22)

где

 − потенциалы соответствующих точек поля, Рисунок 7.

Тогда, из (2.20, 2.21, 2.22)

       (2.23)

Из (2.23) разность потенциалов двух точек поля определяется:

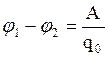  (2.24)

то есть разность потенциалов – это физическая скалярная величина, численно равная работе по перемещению единичного положительного заряда из одной точки поля в другую.

Если же заряд  перемещать из данной точки поля в бесконечность, то работа сил электрического поля равна:

 (2.25)

откуда

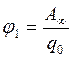 (2.26)

Следовательно, потенциал – это физическая скалярная величина, численно равная работе по перемещению единичного положительного заряда из данной точки поля в бесконечность.

В системе СИ, потенциал и разность потенциалов измеряются в вольтах.

Напряжённость электрического поля измеряется в , .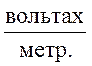

2.4. Конденсаторы.

Устройства, обладающие способностью накапливать значительные заряды, называются конденсаторами. Конденсатор состоит из двух проводников (обкладок), разделённых диэлектриком. Основной характеристикой конденсатора является ёмкость, С.

Под ёмкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов  между его обкладками:

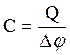        (2.27)

Следовательно, ёмкость характеризует способность конденсатора накапливать заряды.

В зависимости от формы обкладок конденсаторы делятся на: плоские, сферические, цилиндрические, а в зависимости от типа диэлектрика делятся на: воздушные, слюдяные, керамические, электролитические и т.д.

Определим ёмкость плоского конденсатора, обозначив:

S – площадь каждой из пластин конденсатора

σ – поверхностная плотность заряда на каждой из пластин

d – расстояние между пластинами

ξ – относительная диэлектрическая проницаемость диэлектрика, помещённого между пластинами.

Заряд Q на одной из пластин равен:

        (2.28)

Разность потенциалов  между пластинами:

     (2.29)

где Е – напряжённость электрического поля конденсатора.

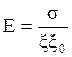        (2.30)

где ξ₀ – электрическая постоянная.

Из формул (2.27 – 2.30) следует, что ёмкость плоского конденсатора равна:

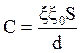      (2.31).

Итак, ёмкость плоского конденсатора:

прямо пропорциональна площади S пластины конденсатора и величине относительной диэлектрической проницаемости ξ диэлектрика между пластинами;

обратно пропорционально расстоянию d между пластинами.

Если n конденсаторов  соединены параллельно, то общая ёмкость:

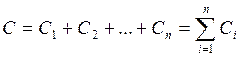         (2.32).

Если n конденсаторов  соединены последовательно, то общая ёмкость С находится из выражения:

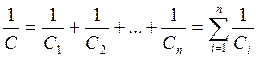      (2.33)

то есть в данном случае суммируются не сами значения емкостей, а величины им обратные.

Практически, во многих схемах используется смешанное соединение конденсаторов. Помимо ёмкости каждый конденсатор характеризуется напряжением пробоя, которое зависит от типа конденсатора,  формы пластин, свойств и параметров диэлектрика.

Энергия электрического поля конденсатора равна:

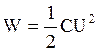   (2.34)

где U – напряжение между пластинами конденсатора, равное значению разности потенциалов .

Из (45, 48) следует:

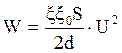         (2.35)

или с учётом:

         (2.36)

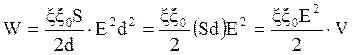(2.37)

где  – объём электрического поля конденсатора.

Объёмная плотность w энергии электрического поля конденсатора определяется:

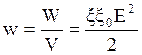      (2.38).

Ёмкость конденсатора измеряется в системе СИ в фарадах (Ф), энергия электрического поля в джоулях (Дж), а объёмная плотность энергии электрического поля в .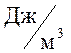

Конденсаторы очень широко применяются в различных электротехнических, радиотехнических и электронных схемах.

3. Электрический ток.

3.1 Законы постоянного электрического тока.

Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. В проводниках I рода (металлы и их сплавы) ток обусловлен упорядоченным движением свободных электронов.

Количественной мерой электрического тока являются: сила тока I, плотность тока .

Сила тока I – это физическая скалярная величина, численно равная величине заряда dq, переносимого через сечение проводника dS за одну секунду.