Законы механики Ньютона. Понятие замкнутой системы. Электростатика. Электрический ток. Электромагнетизм. Понятие магнитного потока. Индукция, страница 3

Величина  выражает алгебраическую сумму зарядов, охватываемых замкнутой поверхностью.

В качестве примера применения теоремы Остроградского-Гаусса рассмотрим расчет напряжённости электрического поля линейно заряженной нити с линейной плотностью  на расстоянии r от нити.

Рисунок 5                               

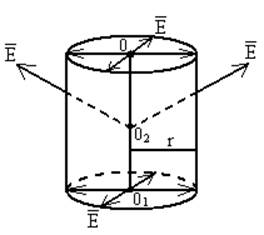Замкнутой поверхностью, заключающей в себе заряженную нить ОО₁ (Рисунок 5) является цилиндрическая поверхность, в которой ось совпадает с нитью. Силовые линии вектора  пересекают только боковую поверхность цилиндра и не пересекают основание цилиндра. Радиус цилиндра совпадает с расстоянием r от нити до точки А, в которой надо вычислить напряжённость поля, созданного линейно заряженной нитью.

Для данного случая поток вектора  равен:

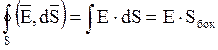 (2.6)

где площадь боковой поверхности цилиндра равна:

(2.7)

где h – высота цилиндра, равная длине нити l = OO₁.

Из (2.6, 2.7)

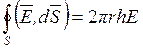      (2.8)

Суммарный заряд нити равен:

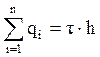   (2.9)

Тогда, с учётом (2.7, 2.8, 2.9) на основании теоремы Остроградского-Гаусса получим что:

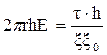 (2.10)

откуда

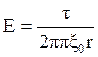   (2.11)

Из (2.11) следует, что напряжённость Е электрического поля линейно заряженной нити: прямо пропорциональна линейной плотности заряда  нити и обратно пропорциональна расстоянию r от нити, а также зависит от диэлектрических свойств среды, т.е. от величины ξ.

В качестве второго примера применения теоремы Остроградского-Гаусса рассмотрим расчёт напряжённости электрического поля вблизи заряженной сферы с поверхностной плотностью заряда , радиусом R на расстоянии r от центра сферы (при условии r>R), Рисунок 6.

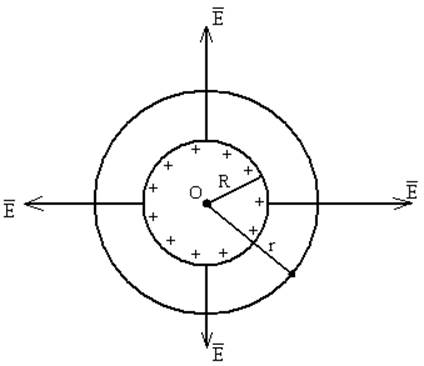Замкнутой поверхностью, заключающей в себе заряженную сферу, является сферическая поверхность радиусом r, которой принадлежит точка А, в которой необходимо определить напряжённость электрического поля, созданного заряженной сферой радиуса R. Обе сферы имеют общий центр в точке О. Как видно из Рисунок 6. силовые линии вектора  заряженной сферы пересекают поверхность построенной сферы радиуса r, а следовательно поток вектора Е через построенную сферу равен:

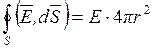    (2.12).

Суммарный заряд поверхностно заряженной сферы равен:

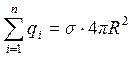        (2.13)

Тогда по теореме Остроградского-Гаусса из (2.5, 2.12, 2.13) следует:

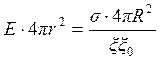   (2.14)

откуда

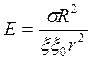    (2.15).

Из расчётной формуле (2.15) следует что напряжённость электрического поля вблизи поверхностно заряженной сферы радиусом R на расстоянии r от её центра (r>R) прямо пропорциональна поверхностной плотности заряда  и квадрату её радиуса R², обратно пропорциональна квадрату расстояния от центра сферы до данной точки поля. Также значение напряжённости электрического поля зависит от диэлектрических свойств среды, то есть от . В частном случае, если точка А находится внутри поверхностно заряженной сферы (r<R), напряжённость электрического поля в этой точке равна нулю, так как внутри такой сферы заряды отсутствуют.

2.3. Работа по перемещению заряда. Потенциал. Разность потенциалов.

Пусть точечный заряд  перемещается из точки 1 в точку 2 в электростатическом поле, созданном другим точечным зарядом ,  Рисунок 7

Рисунок 7.

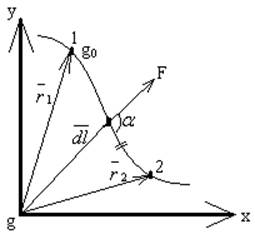Обозначим:  – сила, действующая на заряд  со стороны заряда .  – элементарное перемещение.  – радиусы-векторы, характеризующие положение заряда  в точках 1, 2.  – угол между , .  − работа силы F на элементарном перемещении , равная

       (2.16).

По закону Кулона:

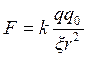     (2.17).

Учтём, что

  (2.18)

Из (2.16, 2.17, 2.18)

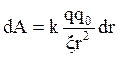          (2.19).

Тогда, работа при перемещении заряда  в поле заряда  из точки 1 в точку 2 равна:

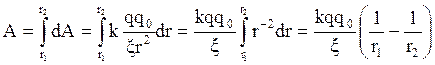      (2.20)

Из формулы (2.20) следует, что:

1. работа по перемещению заряда  не зависит от формы траектории, по которой перемещается заряд .

2. работа по перемещению заряда  по замкнутой траектории равно 0.

3. значение работы определяется: значениями зарядов , , начальным и конечным расстояниями  и  между зарядами; а также зависит от диэлектрических свойств среды.

Следовательно, электростатическое поле точечного заряда  является потенциальным, а кулоновская сила взаимодействия зарядов ,  является консервативной.