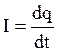(3.1)
Единица силы тока – ампер (А).
Плотность тока 
–
это физическая векторная величина, численно равная силе тока, проходящего через
единицу поперечного сечения проводника, перпендикулярного направлению тока.
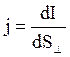(3.2).
Направление совпадает
с направлением скорости упорядоченного движения положительных зарядов.
Следовательно, в проводниках 1 рода направление j противоположно скорости
упорядоченного движения свободных электронов.
Единица плотности
тока –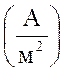 
.
Известны ряд законов постоянного тока: закон Ома для участка цепи и для полной цепи, закон Джоуля-Ленца, законы Кирхгофа.
Закон Ома для участка цепи:
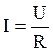(3.3)
где
U – напряжение на участке, R – сопротивление участка
Для линейного проводника длиной l, площадью поперечного сечения S:
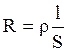(3.4)
где
ρ – удельное сопротивление проводника
Закон Ома для полной цепи, содержащей внешнее сопротивление R, источник тока с заданной ЭДС, ξ и внутреннее сопротивление r:
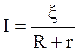(3.5)
В частности, если
источник тока замкнут сам на себя, то есть R=0, то в цепи возникает ток короткого
замыкания 
.
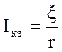(3.6)
В дифференциальной
форме закон Ома выражается для плотности тока j, через: удельную
электропроводность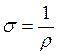 
и
величину E напряжённости электрического поля в проводнике:
(3.7)
Закон Джоуля-Ленца, характеризующий количество тепла Q, выделенное в проводнике сопротивлением R, при прохождении тока I за время t.
С учётом (3.3)
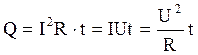(3.8).
В дифференциальной форме закон Джоуля-Ленца характеризует удельную тепловую мощность тока w (количество тепла, выделенное за 1 секунду в 1 объёма проводника при прохождении тока по проводнику):
(3.9).
Законы Кирхгофа.
Первый закон Кирхгофа используется для узла: сумма токов в узле равна 0, то есть
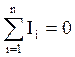(3.10)
При составлении указанной суммы (3.10) условно считают все входящие токи в узел – положительными, а выходящие – отрицательными.
Второй закон Кирхгофа используется для замкнутых контуров: сумма падений напряжений в замкнутом контуре равна сумме ЭДС источников, действующих в контуре:
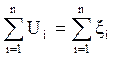(3.11)
При составлении уравнений по второму закону Кирхгофа используется правило обхода по контуру: если направление тока в контуре совпадает с направлением обхода пот контуру, то ток берётся со знаком (+), если не совпадает, то со знаком (–). Значение ЭДС источника берётся со знаком (+), если при выбранном направлении обхода по контуру идут от положительной клеммы источника к отрицательной клемме во внешней цепи. В обратном случае значение ЭДС берут со знаком (–).
3.2 Виды соединений резисторов.
Если n
резисторов: 
соединены
последовательно, то ток в цепи I и ток в каждом из резисторов одинаковы:
а напряжение в общей цепи резисторов равно сумме напряжений на отдельных резисторах:
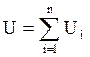(3.13)
Используя закон Ома для участка цепи (3.3) получим из (3.13):
(3.14)
а с учётом (3.12)
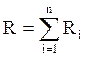(3.15).
Следовательно, общее сопротивление последовательно соединённых резисторов, равно сумме сопротивлений этих резисторов.
Если n
резисторов соединены
параллельно, то напряжение на отдельном резисторе 
и
общее сопротивление U одинаковы:
(3.16), а сила тока I в
общей цепи равна сумме токов Ii в отдельных резисторах
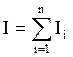(3.17)
Используя закон Ома для участка цепи (3.3) получим из (3.17)
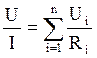(3.18).
С учётом (3.16) получим:
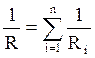(3.19).
Следовательно, при параллельном соединении резисторов складываются не сами сопротивления резисторов, а величины им обратные.
В реальных схемах часто используют смешанное сопротивление резисторов.
3.3. Виды соединений источников тока.
Пусть n одинаковых источников с ЭДС ξ1, внутренним сопротивлением r1, каждый соединены последовательно и замкнуты на внешнее сопротивление R., рис. 8.
Рисунок 8.
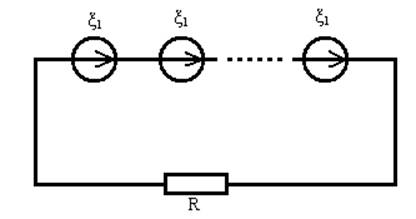Общее значение ЭДС,
ξ, равно:
(3.20)
Общее значение внутреннего сопротивления
(3.21)
Ток I во внешней цепи по закону Ома для полной цепи (3.5) равен:
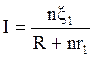(3.22).
Пусть n одинаковых источников с ЭДС ξ1, и внутренним сопротивлением r1 каждый, соединены параллельно и замкнуты на внешнее сопротивление R, Рисунок 9.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.