По закону сохранения энергии:
![]() (13)
(13)
где
![]() (14).
(14).
Из (7, 13, 14) получим:
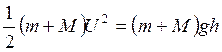 (3.1)
(3.1)
или
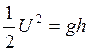 (3.2)
(3.2)
Подставим (4) в (3.2)
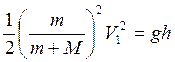 (3.3).
(3.3).
Из (10, 17) получим:
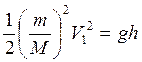 (3.4)
(3.4)
откуда
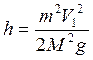 (3.5)
(3.5)
где 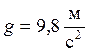 .
.
Вычислим по (12, 19)
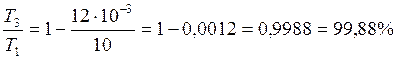
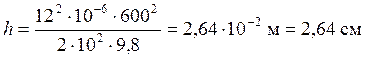
Ответ: 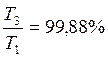 ;
;
![]()
Задача №3.
Два точечных заряда ![]() ,
,
![]() находятся
на расстоянии 60см друг от друга в вакууме. Определить: результирующую
напряжённость в точке, отстоящей от каждого из зарядов на одинаковое расстояние
60см.
находятся
на расстоянии 60см друг от друга в вакууме. Определить: результирующую
напряжённость в точке, отстоящей от каждого из зарядов на одинаковое расстояние
60см.
|
Дано:
|
Рис.
|
|
Е-? |
На рис. Показана
точка А, в которой необходимо найти результирующую напряжённость электрического
поля ![]() .
.
Из рис. По теореме косинуса:
![]() (1)
(1)
где
![]() −
значения напряжённостей, созданных зарядами
−
значения напряжённостей, созданных зарядами ![]() ,
,
![]() −
угол между
−
угол между ![]() .
.
Так как расстояние ![]() ,
то
,
то ![]()
![]() .
.
Учтём, что для
точечных зарядов ![]() выражения
выражения
![]() имеют
вид:
имеют
вид:
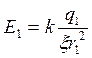 (2)
(2)
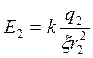 (3)
(3)
где
ξ=1 (относительная диэлектрическая проницаемость вакуума).
k – коэффициент пропорциональности, равный в системе
СИ: 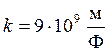 .
.
По условию: ![]() ,
,
![]() .
.
Значит,
![]() (4).
(4).
Из (1, 4) с учётом 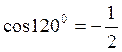
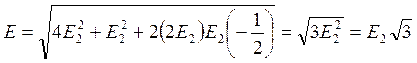 (5).
(5).
Из (3, 4):
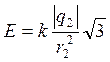 (6)
(6)
Вычисление по (6)
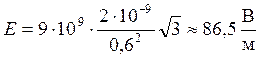
Ответ: 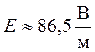
Задача №4.
Электростатическое
поле создано положительно заряженной бесконечной нитью с линейной плотностью ![]() .
Какую скорость приобретёт электрон, приблизившись к нити вдоль линии
напряжённости с расстояния 4 см от нити до 2
см до нити.
.
Какую скорость приобретёт электрон, приблизившись к нити вдоль линии
напряжённости с расстояния 4 см от нити до 2
см до нити.
|
Дано:
|
Рис.
|
|
V-? |
На рис. Показана линейно заряженная нить. Электрон, двигаясь вдоль линии напряжённости, переходит из положения 1 в положение 2., при этом скорость электрона увеличится от 0 до V.
Работа поля по перемещению электрона равна кинетической энергии Т, которую электрон приобретёт в точке 2, то есть:
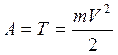 (1)
(1)
где m –
масса электрона; ![]() .
.
Из (1) 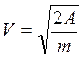 (2)
(2)
Обозначим F – силу, действующую на электрон со стороны электрического поля, созданного заряженной нитью.
![]() (3)
(3)
где e –
заряд электрона; ![]()
Е – напряжённость электрического поля.
Учтём, что для нити с линейной плотностью заряда τ,
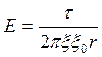 (3)
(3)
где 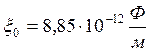 −
электрическая постоянная.
−
электрическая постоянная.
ξ=1 (относительная диэлектрическая проницаемость воздуха).
Из (3, 4)
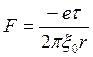 (5).
(5).
Учтём, что работа А по перемещению электрона в электрическом поле линейно заряженной нити с учётом (5) равна:
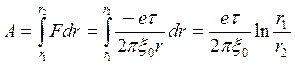 (6)
(6)
Из (2, 6) получим для скорости электрона
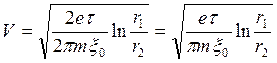 (7).
(7).
Вычислим по (7)
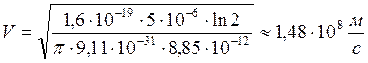 .
.
Вывод размерности по (7):
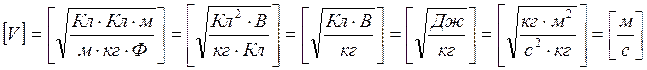
Ответ: 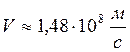
Задача №5.
Тонкий стержень
длиной ![]() расположенный
вертикально и заряжен с линейной плотностью
расположенный
вертикально и заряжен с линейной плотностью 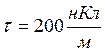 .
Найти напряжённость электрического поля в точке, находящейся на расстоянии
.
Найти напряжённость электрического поля в точке, находящейся на расстоянии ![]() от
нижнего конца стержня на продолжении его длины. Какая сила будет действовать на
заряд 8 нКл, расположенный в этой точке.
от
нижнего конца стержня на продолжении его длины. Какая сила будет действовать на
заряд 8 нКл, расположенный в этой точке.
|
Дано:
|
Рис.
|
|
Е-? F-? |
На рисунке показан тонкий линейный стержень, длиной l. На продолжении стержня в точке А расположен заряд q. Так как стержень не является точечным зарядом, то для определения в точке А напряжённости Е электрического поля разобьём стержень на малые элементы dr с зарядом:
![]() (1).
(1).
Тогда напряжённость dE, созданная зарядом dq с учётом (1) равна:
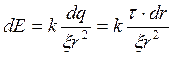 (2)
(2)
где k –
коэффициент пропорциональности, ![]()
![]() .
.
Результирующая напряжённость Е электрического поля, созданного всей заряженной нитью равна с учётом принципа суперпозиции:
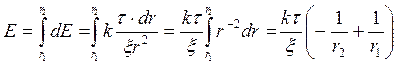 (3).
(3).
Для воздуха ξ=1;
По условию считаем,
что ![]() .
.
Сила F, действующая на заряд q, расположенный в точке А, равна:
![]() (4).
(4).
Вычислим по (3, 4):
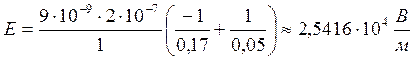
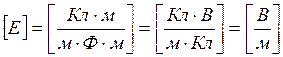
![]()
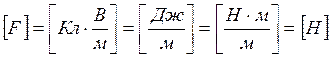
Ответ: 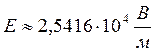 ;
;
![]()
Задача №6.
Плоский конденсатор
состоит из двух слоёв диэлектриков: фарфора с относительное диэлектрической
проницаемостью ![]() и
толщиной
и
толщиной ![]() и
эбонита с относительное диэлектрической проницаемостью
и
эбонита с относительное диэлектрической проницаемостью ![]() и
толщиной
и
толщиной ![]() .
.
Определить ёмкость
конденсатора, если площадь пластин ![]()
|
Дано:
|
Рис.
|
|
С-? |
Данный конденсатор
ёмкостью С является сложным и состоит из двух емкостей ![]() ,
которые соединены последовательно. Следовательно,
,
которые соединены последовательно. Следовательно,
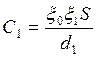 (1)
(1)
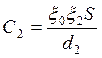 (2)
(2)
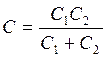 (3).
(3).
Из (1 − 3)
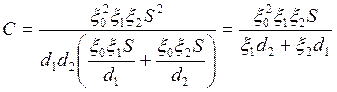 (4)
(4)
где
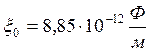 .
.
Упростим (4),
разделив на ![]() :
:
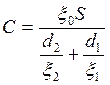 (5)
(5)
Вычислим по (5):
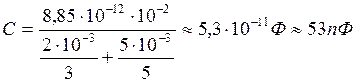
Ответ: ![]()
Задача №7.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.