Эдс батареи ![]() ,
сопротивления:
,
сопротивления: ![]() ,
,
![]() ,
,
![]() ,
сопротивление вольтметра
,
сопротивление вольтметра ![]() .
Какое напряжение покажет вольтметр? Определить токи в резисторах
.
Какое напряжение покажет вольтметр? Определить токи в резисторах ![]() и
в вольтметре.
и
в вольтметре.
|
Дано:
|
Схема:
|
|
|
Задачу можно решить
используя законы Кирхгофа для узла и для замкнутого контура. Предварительно,
обозначим соответствующие токи ![]() ;
обозначим узел А. Возьмём направление обхода контуров по часовой стрелке.
;
обозначим узел А. Возьмём направление обхода контуров по часовой стрелке.
Составим уравнение.
Для узла А по I закону Кирхгофа:
![]() (1)
(1)
По второму закону Кирхгофа для контура, состоящего из эдс ξ, R1, вольтметра V:
![]() (2)
(2)
для контура, состоящего из R3, R2, вольтметра V:
![]() (3)
(3)
Из условия подставим
известные значения в составленные уравнения и решим систему уравнений
относительно токов ![]()
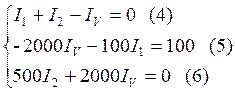
После сокращений получим:
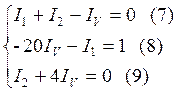
Из (7)
![]() (10)
(10)
Подставим (10) в (8)
![]() или
или
![]() (11)
(11)
Решим совместно (9, 11)
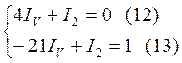
откуда
![]() (14)
(14)
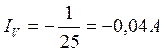
Из (12) ![]()
Из (8) ![]()
Выполним проверку для
найденных значений токов ![]() ,
подставив в (4)
,
подставив в (4)
![]()
![]()
![]() ,
то есть
,
то есть
0=0 (15)
Полученное тождество (15) доказывает правильность расчётов токов.
Зная ![]() ,
,
![]() ,
определим значения напряжения на вольтметре
,
определим значения напряжения на вольтметре ![]() .
Знаки «минус» в токах
.
Знаки «минус» в токах ![]() указывают
на то, что направления указанных токов, взятых произвольно, неверны;
действительные токи направлены обратно взятым направлениям.
указывают
на то, что направления указанных токов, взятых произвольно, неверны;
действительные токи направлены обратно взятым направлениям.
![]() (16)
(16)
или ![]()
Ответ: ![]()
![]()
![]()
![]()
Задача №8.
Элемент замыкают
сначала на внешнее сопротивление ![]() ,
а затем на внешнее сопротивление
,
а затем на внешнее сопротивление ![]() .
В каждом из этих случаев мощность, выделяющаяся во внешней цепи, одинакова и
равна
.
В каждом из этих случаев мощность, выделяющаяся во внешней цепи, одинакова и
равна ![]() .
Найти эдс источника и его внутреннее сопротивление. Чему равен ток короткого
замыкания.
.
Найти эдс источника и его внутреннее сопротивление. Чему равен ток короткого
замыкания.
|
Дано:
|
Мощность тока выразим через силу тока I, сопротивление R
откуда
Для каждого из сопротивлений R1 и R2 найдём соответствующие токи I1, I2 по (2)
|
|
ξ - ? r - ? Iкз |
Используем закон Ома для полной цепи для каждого из сопротивлений R1 и R2
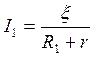 (5)
(5)
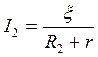 (6)
(6)
или с учётом
известных значений ![]() :
:
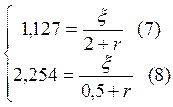
где r – внутреннее сопротивление источника
ξ – эдс источника
Решим систему уравнений (7, 8) относительно ξ, r, разделив уравнения (8, 7)
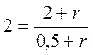 или
или
![]() (9)
(9)
или:
![]()
![]()
Ток короткого замыкания вычисляется по закону Ома при условии R=0, то есть
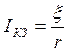 (10)
(10)
или 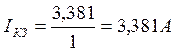
Ответ: ![]()
![]()
![]()
Задача №9.
Из проволоки длиной ![]() сделана
квадратная рамка, по которой течёт ток
сделана
квадратная рамка, по которой течёт ток ![]() .
Найти индукцию и напряжённость магнитного поля в центре рамки.
.
Найти индукцию и напряжённость магнитного поля в центре рамки.
|
Дано:
|
Рис.
|
|
В - ? Н – ? |
На рис. Изображена
квадратная рамка со стороной а, по которой идёт ток I.
Обозначим центр рамки в точке О. Все четыре стороны квадратной рамки имеют
одинаковую длину а и отстоят от т. О на расстояние ![]() .
Следовательно, каждая из сторон при протекании тока I
создаёт напряжённость и индукцию магнитного поля в точке О, как
.
Следовательно, каждая из сторон при протекании тока I
создаёт напряжённость и индукцию магнитного поля в точке О, как ![]() ,
,
![]() ,
а результирующие значения напряжённости Н, индукции В магнитного поля равны:
,
а результирующие значения напряжённости Н, индукции В магнитного поля равны:
![]() (1)
(1)
![]() (2)
(2)
По правилу буравчика ![]() направлены
в точке О перпендикулярно плоскости рамки от нас (при направлении тока I по
часовой стрелке).
направлены
в точке О перпендикулярно плоскости рамки от нас (при направлении тока I по
часовой стрелке).
Для одной из сторон рамки, считая её линейным проводником конечной длины с учётом рис.:
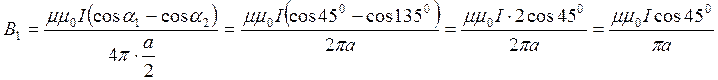 (3)
(3)
Считаем μ=1 (относительная магнитная проницаемость воздуха).
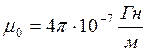 −
магнитная постоянная.
−
магнитная постоянная.
Из (2, 3)
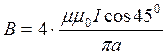 (4)
(4)
где 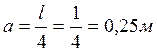
Учитывая связь В, Н имеем:
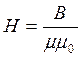 (5)
(5)
Вычислим по (4, 5)
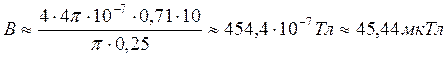
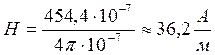
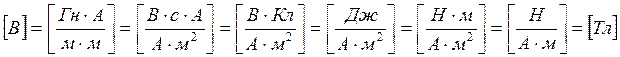
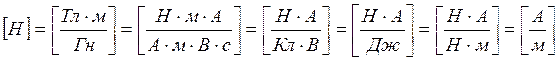
Ответ: ![]()
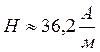
Задача 10.
Сколько ампер-витков
потребуется для того, чтобы внутри соленоида малого диаметра и длиной ![]() объёмная
плотность энергии магнитного поля была равна
объёмная
плотность энергии магнитного поля была равна 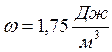 .
.
|
Дано:
|
Если по соленоиду идёт ток I, а общее число витков соленоида N, то число ампер-витков равно (IN). По условию диаметр соленоида намного меньше его длины, то есть соленоид считается бесконечно-длинным (рис)
|
|
(IN)-? |
Обозначим: L – индуктивность соленоида
W – энергия магнитного поля соленоида
V – объём магнитного поля соленоида, длиной l, площадью поперечного сечения S; причём
![]() (1)
(1)
Учтём, что
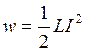 (2)
(2)
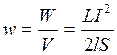 (3)
(3)
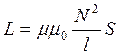 (4)
(4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.