![]() (5.25)
(5.25)
где ξ0 – амплитудное значение эдс.
Уравнения установившихся вынужденных колебаний имеют вид:
лля механических колебаний:
![]() (5.26)
(5.26)
где А – амплитуда вынужденных колебаний
ω – круговая (или циклическая) частота вынужденных колебаний
φ – фаза вынужденных колебаний.
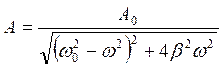 (5.27)
(5.27)
где А0 – начальная амплитуда
β – коэффициент затухания
ω0 – круговая (или циклическая) частота собственных колебаний.
для электромагнитных колебаний:
![]() (5.28)
(5.28)
где
q0 – амплитудное значение заряда на одной из пластин конденсатора в колебательном контуре.
Аналогично (5.27)
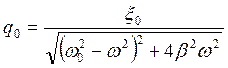 (5.28).
(5.28).
Характерным явлением для вынужденных колебаний является резонанс: резкое возрастание амплитуды вынужденных колебаний. Условием резонанса является равенство:
![]() (5.29)
(5.29)
где
ωрез – резонансная круговая (циклическая) частота
Для определения ωрез исследуем формулу (5.27) или аналогичную формулу (5.28) на максимум. Для этого продифференцируем выражение знаменателя в (5.28) по частоте ω, приравняв результат нулю.
![]() (5.30)
(5.30)
Из (5.30)
![]() (5.31).
(5.31).
Из (5.31)
![]() (5.32).
(5.32).
Следовательно, резонансная частота, как для механических, так и для электромагнитных колебаний равна:
![]() (5.33)
(5.33)
С учётом параметров системы:
для механических колебаний:
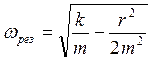 (5.34)
(5.34)
для электромагнитных колебаний:
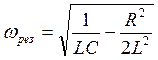 (5.35)
(5.35)
На рис. 25 приведён ряд резонансных кривых для различных коэффициентов затухания β.
Рисунок 25.
![]()
β1>β2>β3
Итак, между вынужденными механическими и Электромагнитными колебаниями много общего. Имеется возможность расчёта резонансной частоты, связанной с параметрами механической системы или с параметрами реального колебательного контура.
II Примеры решения задач по физике, ч I.
1. Механика.
Задача №1.
Движение точки по
кривой задано уравнениями: ![]() ,
м;
,
м; ![]() ,
м.
,
м.
Найти: Уравнение траектории точки, скорость и полное ускорение в момент времени 0,5 с.
|
Дано:
t=0,5 с |
Решим совместно уравнение x(t) и y(t) и, исключив время t, определим уравнение траектории y(x).
Из (2)
Из (1, 3)
или
|
|
y(x)-? V-? a-? |
Уравнение (5) является уравнением траектории.
Для определения
скорости V точки найдём проекции скорости ![]() и
и
![]() ,
так как
,
так как
![]() (6)
(6)
где ![]() ,
,
![]() определим
через производные:
определим
через производные:
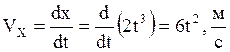 (7)
(7)
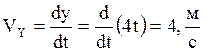 (8)
(8)
В момент времени t=0,5 с,
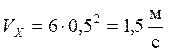
Тогда 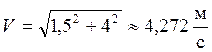 .
.
Аналогично вычисляется ускорение а через проекции ускорения на оси х, у:
![]() (9)
(9)
Значения ![]() ,
,
![]() определяются
через производные:
определяются
через производные:
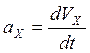 (10)
(10)
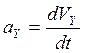 (11)
(11)
или с учётом (7, 8)
![]() (12)
(12)
![]() (13)
(13)
Следовательно,
![]() (14)
(14)
При t=0,5 с,
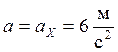 .
.
Ответ: ![]() ;
;
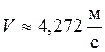 ;
;
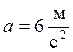 .
.
Задача №2.
Пуля массой 12г летит
горизонтально со скоростью 600![]() ,
попадает в мешок с песком массой 10кг, висящий на длинной нити, и застревает в
нём.
,
попадает в мешок с песком массой 10кг, висящий на длинной нити, и застревает в
нём.
Определить: 1) высоту, на которую поднимается мешок, отклонившись после удара 2) долю кинетической энергии, израсходованной на пробивание песка.
|
Дано:
|
Рис.
|
|
|
Обозначим:
m – масса пули
М – масса мешка с песком
До попадания пули в мешок, пуля обладала импульсом P1
![]() (1)
(1)
где ![]() −
скорость пули.
−
скорость пули.
Удар пули о мешок с песком является абсолютно-неупругим; следовательно импульс мешка с песком с застрявшей пулей равен P2
![]() (2)
(2)
где U – общая скорость тел.
По закону сохранения импульса:
![]() (3)
(3)
откуда
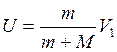 (4)
(4)
Обозначим: Т1 – кинетическая энергия пули до застревания в мешке с песком.
Т2 – кинетическая энергия пули, мешка с песком после застревания.
Т3 – кинетическая энергия, израсходованная на пробивание песка.
По закону сохранения энергии:
![]() (5)
(5)
где
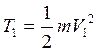 (6)
(6)
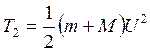 (7).
(7).
Из (5, 6, 7)
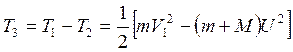
Из (4, 8):
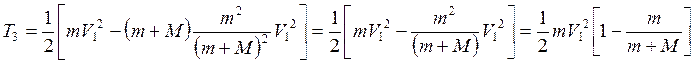 (9)
(9)
По условию ![]() кг,
М=10кг, то есть m<<<M. Следовательно:
кг,
М=10кг, то есть m<<<M. Следовательно:
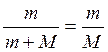 (10)
(10)
Из (9, 10) 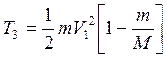 (11).
(11).
Доля кинетической энергии, израсходованной на пробивание песка в мешке, равна:
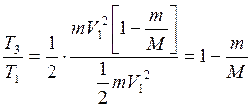 (12).
(12).
Определим высоту h, на которую отклонится мешок с песком и пулей, застрявшей в мешке.
Обозначим:
П – потенциальная энергия мешка с песком и пулей при поднятии на высоту h.
Т2 – кинетическая энергия мешка с пулей при застревании пули в мешке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.