Управление режимами работы электрических двигателей в разомкнутых системах электропривода. Модели двигателей в установившихся режимах, страница 7

·  По (2.9) определяют количество пусковых сопротивлений; если m оказывается не целым числом, его округляют до целого и находят новое значение l;

·  Определяют величины сопротивлений, выключаемых на каждой ступени.

Искомые значения r_п1, r_п2, … определяют как разность сопротивлений на соседних характеристиках:

r_n3=R_n3-r_a=lr_a-r_a=r_a(l-1),

r_n2=R_n2-R_n3=l²r_a-lr_a=r_a(l-1)l,              (2.10)

r_n1=R_n1-R_n2=l³r_a-l²r_a=r_a(l-1)l².

В общем случае для m-ступенчатого пуска

r_nm=r_a(l-1),

-------------                          (2.11)

r_п1=r_a(l-1)l^m-1

Аналогичным способом рассчитываются токоограничивающие сопротивления в тормозных режимах работы двигателя.

Из изложенного следует, что расстояния между соответствующими точками электромеханической характеристики при I=I₁ (точки а, в, д, з, м) пропорциональны соответствующим ступеням сопротивления:

r_a»мз,

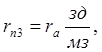
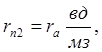
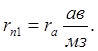
Для точного подбора сопротивлений, особенно при больших тках якоря, приходится составлять сложные схемы соединения секций ящиков сопротивлений [5]. При практической реализации схем реостатного пуска можно допустить некоторые отступления от правильной пусковой диаграммы, так как за счет влияния индуктивности якорной цепи максимальные значения токов не достигают I₁ (пунктирная диаграмма).

2.2  Ограничения тока якоря двигателей постоянного тока с последовательным и смешанным возбуждением изменением сопротивления якорной цепи.

Причины возникновения недопустимых токов аналогичны соответствующим причинам, характерным для двигателей с независимым возбуждением. Однако в связи с нелинейностью электромеханических характеристик метод расчета пусковых сопротивлений отличается от рассмотренного в п.2.1.

Рассмотрим расчет пусковых сопротивлений для двигателей с последовательным возбуждением. При расчете сопротивлений для двигателя со смешанным возбуждением используется тот же метод.

Предположим, что правильная пусковая диаграмма построена (обычно эта диаграмма строится итерационным методом) и рассмотрим зависимость w(R_a) при I=I₁=const.

При неизменности тока якоря поток возбуждения так же не изменится. Следовательно, зависимость w(R_а), соответствующая условию I=I₁=const, является линейной. Для построения этой зависимости рассмотрим работу двигателя в точках а₁ и з₁.

 

	Рис. 2.3

 

При работе двигателя в точке а₁ ток якоря определяется только величинами приложенного напряжения и пускового сопротивления R_п1. Следовательно,

R_n1=U/I₁                            (2.12)

Точка з₁ соответствует естественной характеристике. Следовательно, в этом случае сопротивление якорной цепи равно внутреннему сопротивлению двигателя r_а.

Откладывая по оси R_а величины R_п1 и r_а и учитывая значения скорости, которые этим сопротивлениям соответствуют, строим зависимость w(R_а) при I=I₁=const (рис.2.3). перенесем на эту прямую точки в₁ и д₁ и получим точки в₂ и д₂. сопротивления для характеристик 1 и 2 отличаются на величину r_п1 первой ступени пускового сопротивления. Следовательно, в координатах w, R_а r_п1 соответствует отрезку а₂в₃. аналогичным образом определяются сопротивления для других ступеней.

Можно посмотреть также прямую w(R_a) при  I=I₂=const. Эта прямая при расчете сопротивлений не используется, но полезнв для понимания сути протекающих процессов.

Движению рабочей точки по характеристике 1 от точки а₁ до точки б₁ соответствует постоянное значение сопротивления якорной цепи, равное R_п1. Следовательно, в координатах w,R_а этому процессу соответствует движение по вертикали а₂б₂. Переходу с точки б₁ в точку в₁ соответствует скачкообразное изменение сопротивления на величину r_п1 при неизменной скорости. В координатах w, R_а рабочая точка переходит из б₂ в в₂. дальнейшие рассуждения аналогичны.